|
Otázce přerovnávání neabsolutně konvergentní řady se věnuje Věta 3.8.
Věta 3.8 (Riemannova). Nechť řada 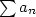 konverguje neabsolutně a nechť konverguje neabsolutně a nechť 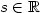 je libovolné. Pak existuje takové přerovnání je libovolné. Pak existuje takové přerovnání 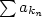 řady řady 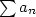 , že , že 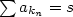 , existuje takové přerovnání , existuje takové přerovnání 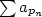 řady řady 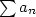 , že , že 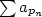 určitě diverguje a takové přerovnání určitě diverguje a takové přerovnání 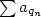 , že řada , že řada 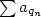 osciluje. osciluje.
Ačkoliv je tato věta v textu dokázána, připomeňme si myšlenku důkazu. Nejdříve si ale ještě připomeňme následující skutečnost (související s Lemmatem 3.2).
Mějme neabsolutně konvergentní řadu 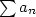 . Potom sestrojíme-li řadu pouze z kladných členů řady . Potom sestrojíme-li řadu pouze z kladných členů řady 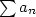 , bude tato řada divergovat. Totéž platí pro řadu sestavenou pouze ze záporných členů řady , bude tato řada divergovat. Totéž platí pro řadu sestavenou pouze ze záporných členů řady 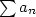 . .
Důkaz tohoto tvrzení by byl témeř totožný s důkazem Lemmatu 3.2. Kdyby konvergovala jen jedna z těchto řad, potom by řada 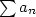 divergovala. Pokud by konvergovaly obě tyto řady, pak by řada divergovala. Pokud by konvergovaly obě tyto řady, pak by řada 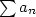 konvergovala absolutně. konvergovala absolutně.
Nyní se ale vraťme k Riemannově větě. Přerovnání řady 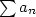 v konvergentní řadu v konvergentní řadu 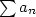 se součtem se součtem  provedeme následovně. Pro jednoduchost předpokládejme, že provedeme následovně. Pro jednoduchost předpokládejme, že  je nezáporné (pro záporné je nezáporné (pro záporné  by byl postup analogický). Začneme nejdříve sčítat kladné členy, dokud součet nepřevýší číslo by byl postup analogický). Začneme nejdříve sčítat kladné členy, dokud součet nepřevýší číslo  . Poté přičítáme záporné členy, dokud není součet nižší než . Poté přičítáme záporné členy, dokud není součet nižší než  . A nyní opět přičítáme kladné členy a tak pořád dokola. To, že součet číslo . A nyní opět přičítáme kladné členy a tak pořád dokola. To, že součet číslo  jednou překročí nám zaručuje již zmíněná divergence řad z kladných (resp. záporných) členů. A protože členy obou těchto řad jdou k nule (což musí, má-li řada jednou překročí nám zaručuje již zmíněná divergence řad z kladných (resp. záporných) členů. A protože členy obou těchto řad jdou k nule (což musí, má-li řada 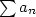 konvergovat), budeme číslo konvergovat), budeme číslo  "překračovat" stále méně a méně. "překračovat" stále méně a méně.
Přerovnání v divergentní řadu 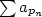 řešme následovně (pro jednoduchost divergenci k řešme následovně (pro jednoduchost divergenci k 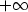 ). Sčítejme kladné členy řady ). Sčítejme kladné členy řady 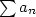 , dokud nepřekročíme číslo 1. Poté přičtěme jeden záporný člen řady , dokud nepřekročíme číslo 1. Poté přičtěme jeden záporný člen řady 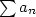 a následně opět kladné členy, dokud nepřekročíme číslo 2, atd. Řada vzniklá tímto způsobem určitě diverguje k a následně opět kladné členy, dokud nepřekročíme číslo 2, atd. Řada vzniklá tímto způsobem určitě diverguje k 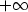 . .
Způsob přerovnání v oscilující řadu 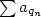 je nyní již zřejmý. Nejdříve sčítáme kladné členy řady je nyní již zřejmý. Nejdříve sčítáme kladné členy řady 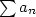 , dokud nepřekročíme čislo 1. Poté budeme přičítat záporné členy, až je součet menší než 0. Následně opět přičítáme kladné členy až překročíme 1 a tak stále dokola. Získali jsme oscilující řadu. , dokud nepřekročíme čislo 1. Poté budeme přičítat záporné členy, až je součet menší než 0. Následně opět přičítáme kladné členy až překročíme 1 a tak stále dokola. Získali jsme oscilující řadu.
Přerovnávání neabsolutně konvergentních alternujících řad si můžete prohlédnout na jednoduchém Java apletu.
| 




