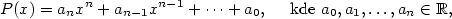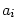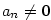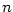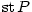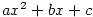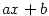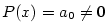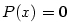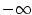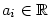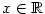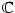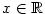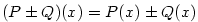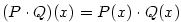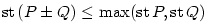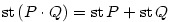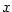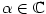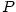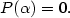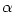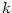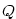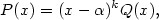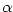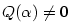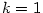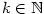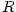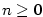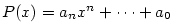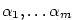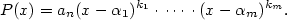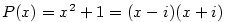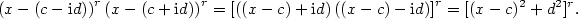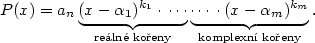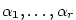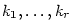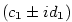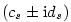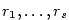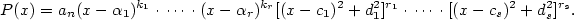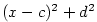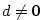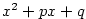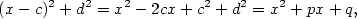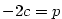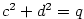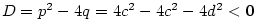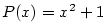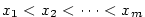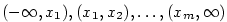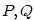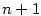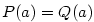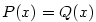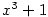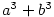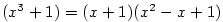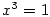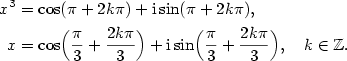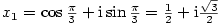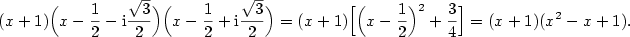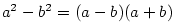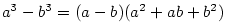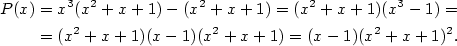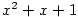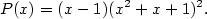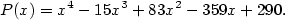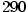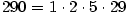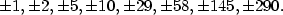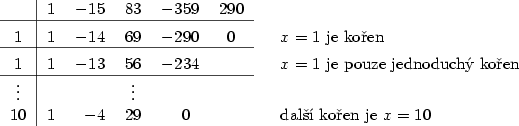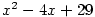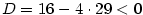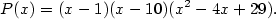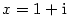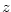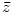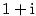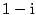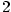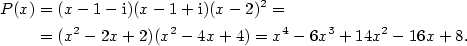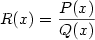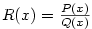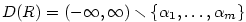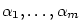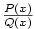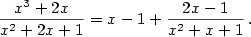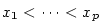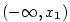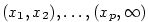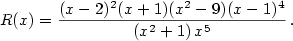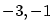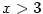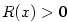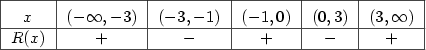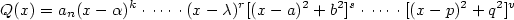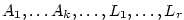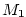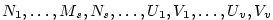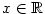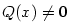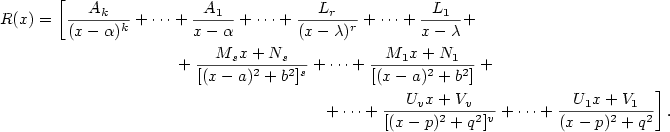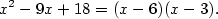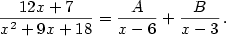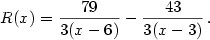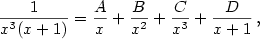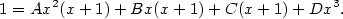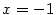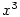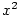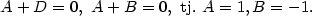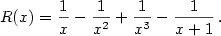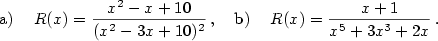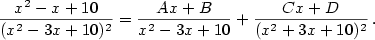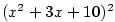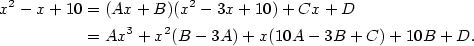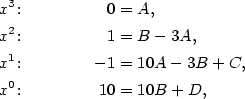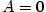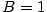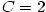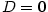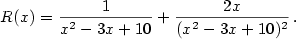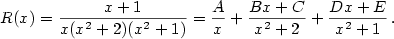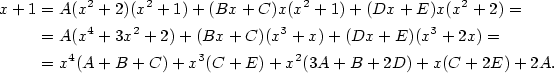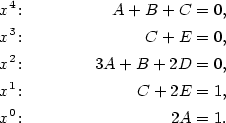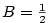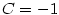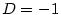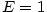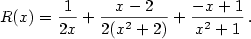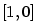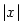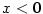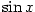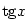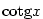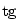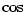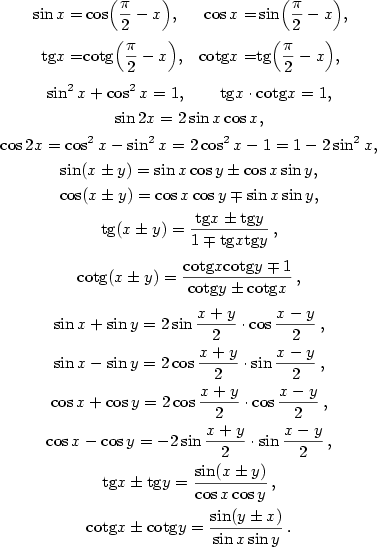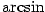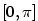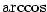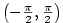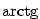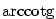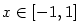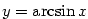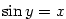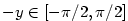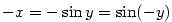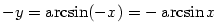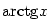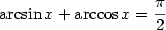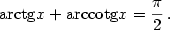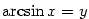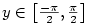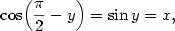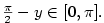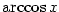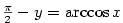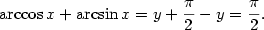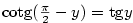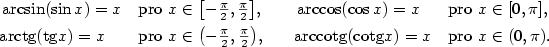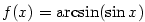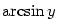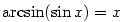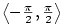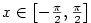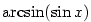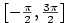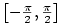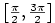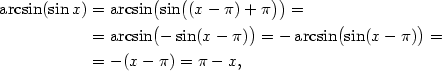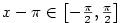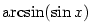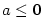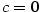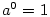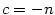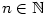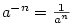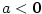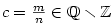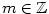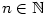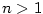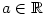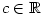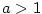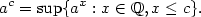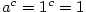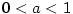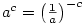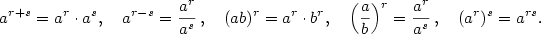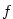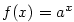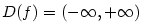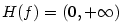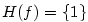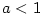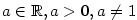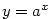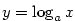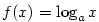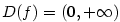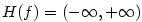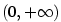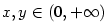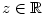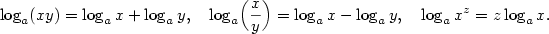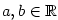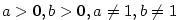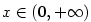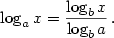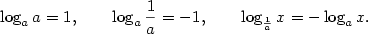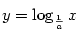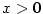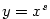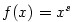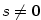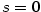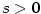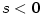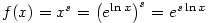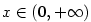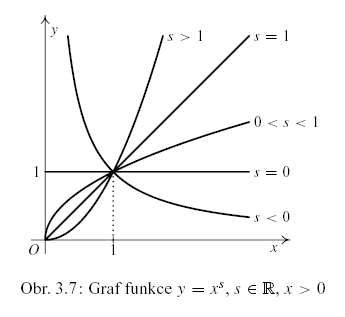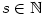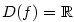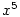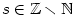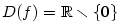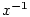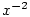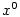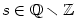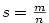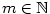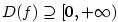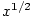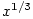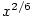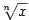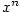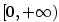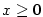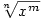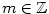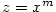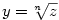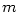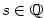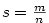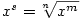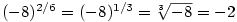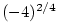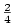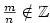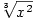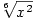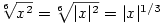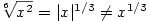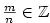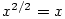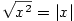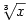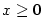Kapitola 3Elementární funkce
V této kapitole zavedeme základní elementární funkce — polynomy, racionální lomené funkce,
goniometrické a cyklometrické funkce, funkce exponenciální, logaritmické a mocninné.
Nejjednoduššími elementárními funkcemi jsou polynomy.
3.1. Polynomy
Příklad 3.2.
Příkladem jsou již ze střední školy známé polynomy:
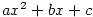 — kvadratický polynom, — kvadratický polynom, 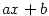 — lineární polynom.
Je-li — lineární polynom.
Je-li 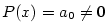 , jde o polynom nulového stupně. Polynom , jde o polynom nulového stupně. Polynom
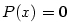 nazýváme nulovým polynomem a přiřazujeme mu jako stupeň
symbol nazýváme nulovým polynomem a přiřazujeme mu jako stupeň
symbol 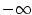 (někdy se mu stupeň nepřiřazuje). (někdy se mu stupeň nepřiřazuje).
|
Poznámka 3.3.
-
Definičním oborem polynomu je množina reálných čísel.
-
Takto definovaný polynom (kde
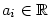 a a 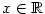 ) se
také nazývá reálným polynomem nad množinou ) se
také nazývá reálným polynomem nad množinou 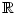 .
Pokud .
Pokud  , mluvíme o reálném polynomu nad množinou , mluvíme o reálném polynomu nad množinou 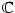 .
Protože v celém textu rozumíme pod pojmem funkce
pouze reálné funkce reálné proměnné,
pod pojmem polynom rozumíme vždy reálný polynom nad .
Protože v celém textu rozumíme pod pojmem funkce
pouze reálné funkce reálné proměnné,
pod pojmem polynom rozumíme vždy reálný polynom nad 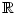 . Podrobněji o polynomech
viz [11]. . Podrobněji o polynomech
viz [11].
-
Mezi polynomy definujeme operace sčítání (resp. odčítání) a násobení tak, že pro každé
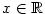 platí
platí 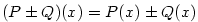 a a 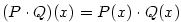 .
Součet (resp. rozdíl) a součin dvou polynomů je opět polynom. Platí .
Součet (resp. rozdíl) a součin dvou polynomů je opět polynom. Platí 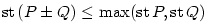 a
a 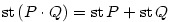 .
Při sčítání (resp. odčítání) sčítáme (resp. odčítáme) koeficienty u stejných mocnin proměnné .
Při sčítání (resp. odčítání) sčítáme (resp. odčítáme) koeficienty u stejných mocnin proměnné 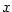 .
Při násobení jde o obyčejné násobení .
Při násobení jde o obyčejné násobení 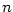 -členů. -členů.
|
Následující tvrzení uvádíme bez důkazů. Teorie polynomů bude podrobněji probírána později v algebře,
viz např. [11].
- Je-li
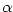 kořen polynomu kořen polynomu 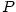 , pak existuje polynom , pak existuje polynom
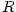 tak, že tak, že  . .
-
Základní věta algebry:
Polynom 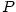 stupně stupně 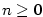 má v má v 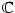 právě právě 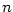 kořenů, počítáme-li každý
kořen tolikrát, kolik je jeho násobnost. kořenů, počítáme-li každý
kořen tolikrát, kolik je jeho násobnost.
Všimněte si, že nulový polynom má za kořen každé číslo.
- Rozklad polynomu v
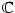 . .
Důsledkem základní věty algebry je:
Je-li
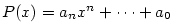 polynom a polynom a 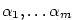 (kde (kde
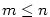 ) jsou všechny jeho navzájem různé kořeny s násobnostmi ) jsou všechny jeho navzájem různé kořeny s násobnostmi 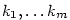 ,
pak ,
pak
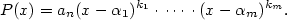
Tento rozklad polynomu 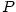 se nazývá rozklad polynomu v se nazývá rozklad polynomu v 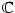 nebo
také rozklad polynomu na součin kořenových činitelů. nebo
také rozklad polynomu na součin kořenových činitelů.
Například 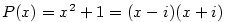 je rozklad v je rozklad v 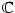 . .
-
Je-li komplexní číslo
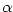 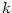 -násobným kořenem reálného polynomu -násobným kořenem reálného polynomu 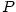 ,
je číslo komplexně sdružené ,
je číslo komplexně sdružené 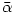 rovněž rovněž 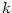 -násobným kořenem polynomu -násobným kořenem polynomu
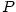 . .
Pro kořenové činitele příslušné komplexním kořenům 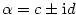 platí
platí
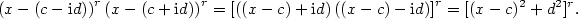
- Rozklad polynomu v
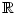 . .
Je-li 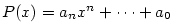 polynom, pak podle základní věty
algebry můžeme polynom, pak podle základní věty
algebry můžeme 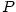 rozložit v rozložit v 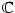 : :
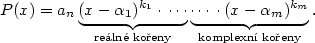
Jsou-li 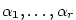 reálné kořeny s násobnostmi reálné kořeny s násobnostmi
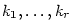 a a 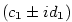 , ..., , ..., 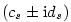 navzájem
různé dvojice nereálných komplexně sdružených kořenů s násobnostmi navzájem
různé dvojice nereálných komplexně sdružených kořenů s násobnostmi
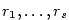 , platí , platí
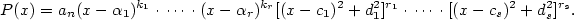
Tento rozklad se nazývá rozklad polynomu v  . .
Poznamenejme, že se někdy kvadratické výrazy 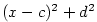 , kde , kde 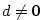 , píší ve tvaru
kvadratických trojčlenů , píší ve tvaru
kvadratických trojčlenů 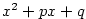 se záporným diskriminantem, neboť se záporným diskriminantem, neboť
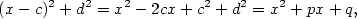
kde 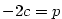 , , 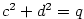 a a 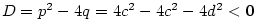 . .
Například, 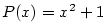 je rozklad je rozklad 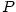 v v 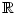 . .
-
Znaménko polynomu — intervaly, kde je polynom kladný, resp.záporný.
Z rozkladu polynomu určujeme znaménko hodnot polynomu.
Je-li
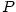 polynom a jsou-li polynom a jsou-li 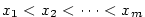 všechny jeho navzájem různé
reálné kořeny s lichou násobností, pak v každém z intervalů všechny jeho navzájem různé
reálné kořeny s lichou násobností, pak v každém z intervalů
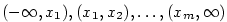 je je 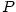 stále nekladný
nebo stále nezáporný. Vybereme-li dva sousední intervaly, pak v jednom z nich jsou
hodnoty nekladné a v druhém nezáporné. stále nekladný
nebo stále nezáporný. Vybereme-li dva sousední intervaly, pak v jednom z nich jsou
hodnoty nekladné a v druhém nezáporné.
-
Jestliže polynomy
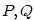 mají stupně nejvýše rovny danému přirozenému číslu mají stupně nejvýše rovny danému přirozenému číslu
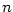 a jestliže existuje a jestliže existuje 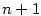 navzájem různých komplexních čísel navzájem různých komplexních čísel 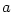 tak, že tak, že
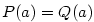 , pak jsou polynomy , pak jsou polynomy 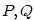 identické, tj. mají
stejné koeficienty, takže rovnost identické, tj. mají
stejné koeficienty, takže rovnost 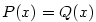 platí pro každé platí pro každé 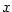 . .
Příklad 3.5.
Rozložte v 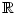 polynom polynom 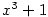 . .
|
Zobrazit / skrýt řešení |
Příklad 3.6.
Rozložte v 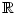 následující polynomy: následující polynomy:
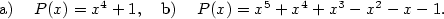
|
Zobrazit / skrýt řešení |
Příklad 3.7.
Proveďte rozklad v 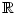 polynomu polynomu
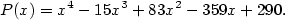
|
Zobrazit / skrýt řešení |
Příklad 3.8.
Nalezněte polynom nejnižšího stupně s reálnými koeficienty, který má kořen 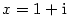 a dvojnásobný
kořen a dvojnásobný
kořen  . .
|
Zobrazit / skrýt řešení |
3.2. Racionální funkce
Příkladem ryze lomené racionální funkce jsou funkce 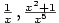 ; příkladem neryze lomené racionální funkce jsou funkce ; příkladem neryze lomené racionální funkce jsou funkce
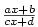 , kde , kde 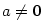 , , 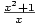 nebo nebo  .
Platí následující tvrzení: .
Platí následující tvrzení:
- Definičním oborem racionální funkce
 je množina tvaru je množina tvaru
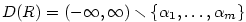 , kde , kde
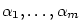 jsou všechny reálné kořeny polynomu jsou všechny reálné kořeny polynomu 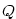 . .
-
Je-li
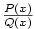 neryze lomená racionální funkce, pak dělením polynomů neryze lomená racionální funkce, pak dělením polynomů
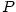 a a 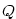 obdržíme součet polynomu a ryze lomené racionální funkce.
Například: obdržíme součet polynomu a ryze lomené racionální funkce.
Například:
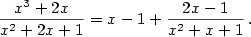
-
Znaménko racionální funkce.
Buď
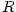 racionální funkce, jejíž čitatel a jmenovatel nemají společné
kořeny. Buďte racionální funkce, jejíž čitatel a jmenovatel nemají společné
kořeny. Buďte 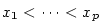 všechny navzájem různé reálné kořeny čitatele
a jmenovatele s lichou násobností. Pak v každém z intervalů všechny navzájem různé reálné kořeny čitatele
a jmenovatele s lichou násobností. Pak v každém z intervalů
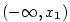 , , 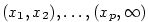 jsou všechny hodnoty jsou všechny hodnoty 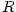 stále nezáporné
nebo nekladné (ve všech bodech, v nichž je stále nezáporné
nebo nekladné (ve všech bodech, v nichž je 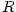 definovaná). V sousedních intervalech
se střídají znaménka. definovaná). V sousedních intervalech
se střídají znaménka.
Příklad 3.10.
Určete všechny maximální intervaly, na kterých mají hodnoty 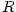 stejné znaménko. stejné znaménko.
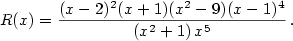
|
Zobrazit / skrýt řešení |
Následující věta má zásadní význam pro integraci racionálních funkcí. Její důkaz
lze nalézt např. v [10, 14].
Zlomky z předchozí věty nazýváme parciální zlomky.
Jsou to ryze lomené racionální funkce speciálních typů.
Poznámka 3.12.
Konstanty v parciálních zlomcích (lze ukázat, že jsou určeny jednoznačně) nalezneme metodou
neurčitých koeficientů, tj. napíšeme
formální tvar rozkladu a celou rovnost vynásobíme polynomem 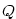 . Dostaneme tak
rovnost dvou polynomů pro všechna . Dostaneme tak
rovnost dvou polynomů pro všechna 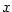 kromě kořenů jmenovatele.
Tyto polynomy jsou proto identické, tj. mají stejné koeficienty, které určíme
pomocí dvou možných způsobů: kromě kořenů jmenovatele.
Tyto polynomy jsou proto identické, tj. mají stejné koeficienty, které určíme
pomocí dvou možných způsobů:
- porovnáním koeficientů u odpovídajících si mocnin,
- dosazením konkrétních hodnot
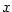 (vhodné jsou zvláště kořeny jmenovatele (vhodné jsou zvláště kořeny jmenovatele 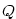 ). ).
Získáme soustavu 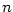 lineárních rovnic pro lineárních rovnic pro 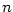 neznámých konstant, kterou vyřešíme. neznámých konstant, kterou vyřešíme.
|
Algoritmus rozkladu racionální funkce:
Neryze lomená racionální funkce —
vydělíme čitatele a jmenovatele a tím získáme polynom a
ryze lomenou racionální funkci, kterou rozložíme následovně:
Ryze lomená racionální funkce — rozložíme
jmenovatele v 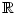 , napíšeme si formální tvar rozkladu na parciální zlomky
a určíme konstanty. , napíšeme si formální tvar rozkladu na parciální zlomky
a určíme konstanty.
Příklad 3.13.
Rozložte na parciální zlomky racionální funkci

|
Zobrazit / skrýt řešení |
Příklad 3.14.
Rozložte na parciální zlomky funkci
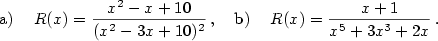
|
Zobrazit / skrýt řešení |
3.3. Goniometrické a cyklometrické funkce
Geometrický význam této definice je znázorněn na obr. 3.1, grafy goniometrických funkcí
na obr. 3.2 a 3.3.
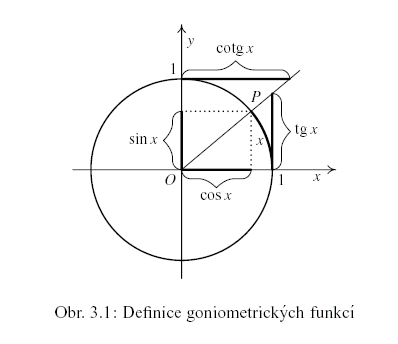
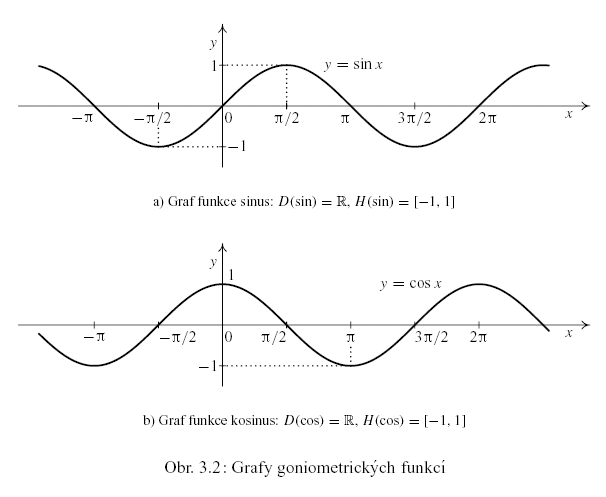
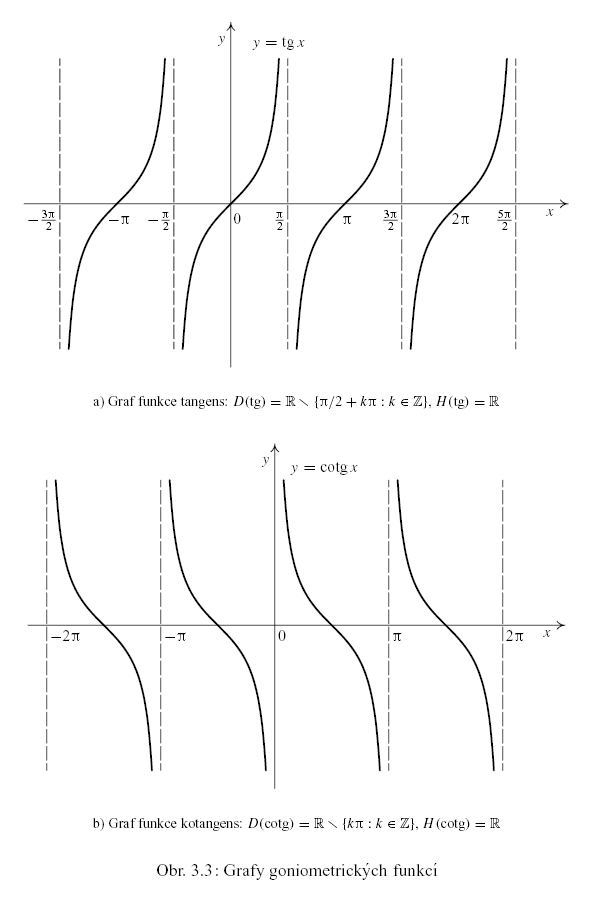
Nabízí se otázka, zda existují inverzní funkce k funkcím
goniometrickým. Protože inverzní funkce existuje pouze k prosté funkci, můžeme
inverzní funkce k funkcím goniometrickým definovat jenom v těch intervalech
definičních oborů goniometrických funkcí, kde jsou tyto funkce ryze monotonní,
a tedy prosté. Výběr intervalů se provádí takto:

Odtud plyne následující definice.
Definice 3.17.
Inverzní funkce k funkci  definované na intervalu definované na intervalu
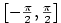 se značí se značí 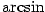 . .
Inverzní funkce k funkci 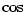 definované na intervalu definované na intervalu
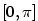 se značí se značí 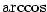 . .
Inverzní funkce k funkci 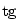 definované na intervalu definované na intervalu
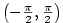 se značí se značí 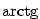 . .
Inverzní funkce k funkci  definované na intervalu definované na intervalu
 se značí se značí 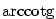 . .
Funkce 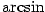 , , 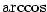 , , 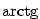 a a 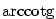 nazýváme
cyklometrické funkce. nazýváme
cyklometrické funkce.
|
Grafy jsou znázorněny na obr. 3.4.
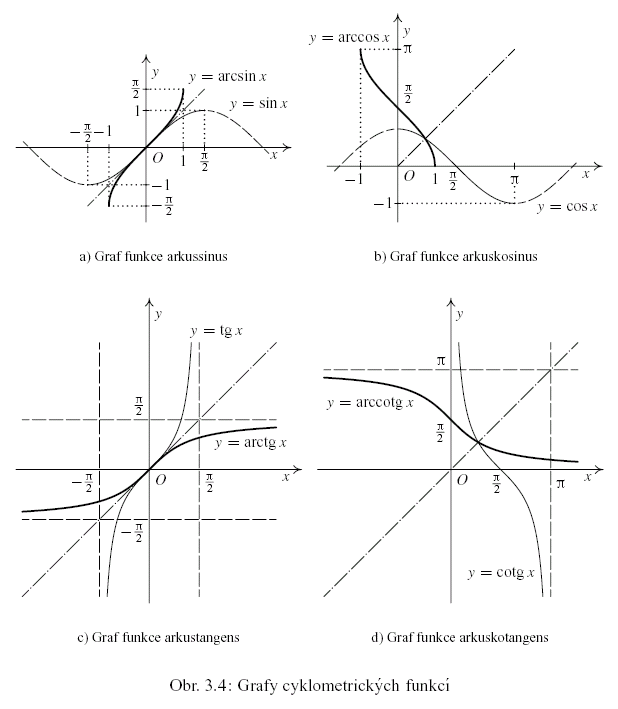
Věta 3.18. Cyklometrické funkce mají následující vlastnosti:
- Funkce
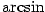 a a 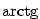 jsou rostoucí, funkce jsou rostoucí, funkce 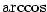 a a
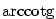 jsou klesající. jsou klesající.
-
Funkce
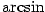 a a 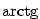 jsou liché. jsou liché.
|
Důkaz.
Tvrzení 1 je zřejmé — plyne z věty 1.46 o inverzní funkci
k funkci ryze monotonní. Stačí dokázat tvrzení 2.
Nechť 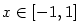 a označme a označme 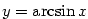 . Pak . Pak 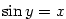 .
Platí .
Platí  , a proto rovněž , a proto rovněž 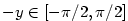 .
Protože funkce .
Protože funkce 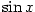 je
lichá, platí je
lichá, platí 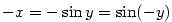 , a tudíž , a tudíž 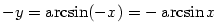 a tvrzení je dokázáno. Podobně pro
a tvrzení je dokázáno. Podobně pro 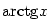 . .
|
Zobrazit / skrýt důkaz |
| Poznámka 3.20.
Vzhledem k definici inverzní funkce platí:
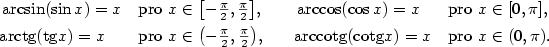
Mimo uvedené intervaly ale rovnosti neplatí — viz následující příklad.
|
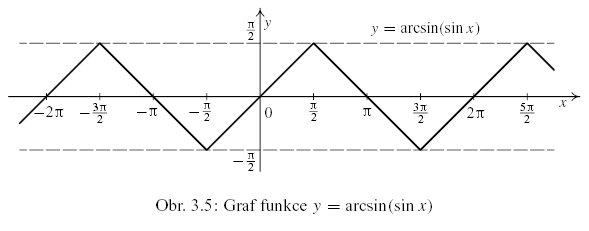
Příklad 3.21.
Nakreslete graf funkce 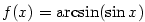 . .
|
Zobrazit / skrýt řešení |
3.4. Exponenciální a logaritmické funkce
Zavedení těchto funkcí je poměrně obtížné, protože nelze aritmetickými operacemi
zavést mocniny s iracionálním exponentem. Je možné postupovat dvěma způsoby:
definovat nejprve funkci logaritmickou jako primitivní funkci k funkci 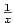 ,
a pak pomocí funkce k ní inverzní zavést funkci exponenciální, nebo definovat nejprve
funkci exponenciální a přes inverzi funkci logaritmickou. Protože první postup vyžaduje
znalosti základů integrálního počtu, z názorných důvodů
zvolíme druhý postup — zavedeme nejprve funkci exponenciální.
Ze střední školy je známo, jak definujeme mocninu ,
a pak pomocí funkce k ní inverzní zavést funkci exponenciální, nebo definovat nejprve
funkci exponenciální a přes inverzi funkci logaritmickou. Protože první postup vyžaduje
znalosti základů integrálního počtu, z názorných důvodů
zvolíme druhý postup — zavedeme nejprve funkci exponenciální.
Ze střední školy je známo, jak definujeme mocninu 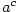 , kde , kde
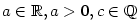 : :
- Pro
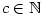 je je 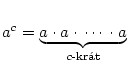 (může být i
(může být i 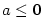 ), pro ), pro 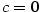 je je 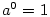 , ,
- pro
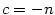 , kde , kde 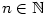 , je , je 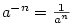 (může být i (může být i 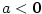 ), ),
- pro
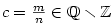 , kde , kde 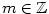 , , 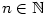 , , 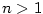 , je , je
 (pro (pro  může být i může být i  ). ).
(Připomeňme, že existence odmocniny byla dokázána v lemmatu 1.14 a rovněž
bylo upozorněno na korektnost definice pro racionální exponent.)
Nyní již můžeme přistoupit k definici mocniny 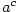 pro libovolné kladné reálné pro libovolné kladné reálné 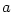 a
libovolné reálné a
libovolné reálné  .
Snadno se ověří, že pro .
Snadno se ověří, že pro 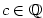 je tato nová definice ve shodě s původní. Rovněž je
možné dokázat pravidla pro počítání s mocninami, známá pro racionální exponenty.
Zejména platí ( je tato nová definice ve shodě s původní. Rovněž je
možné dokázat pravidla pro počítání s mocninami, známá pro racionální exponenty.
Zejména platí (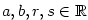 , , 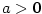 , , 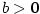 ) )
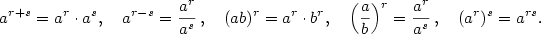
Důkazy viz [17, str. 45], kde lze nalézt i důkazy vět 3.24 a 3.26.
Definice 3.23.
Buď  Funkci Funkci 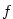 určenou předpisem určenou předpisem 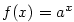 nazveme
exponenciální funkcí o základu nazveme
exponenciální funkcí o základu 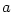 . .
|
Největší význam z exponenciálních funkcí má funkce o základu 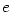 (Eulerovo
číslo — viz definice 2.27), tj. funkce (Eulerovo
číslo — viz definice 2.27), tj. funkce 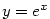 . .
Věta 3.24.
Exponenciální funkce 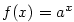 má tyto vlastnosti: má tyto vlastnosti:
-
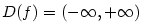 a a 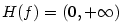 pro pro 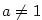 , , 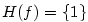 pro pro 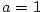 . .
- Funkce
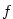 je rostoucí v je rostoucí v 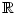 pro pro 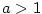 , klesající v , klesající v 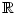 pro pro 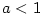 (viz obr. 3.6)
a konstantní v (viz obr. 3.6)
a konstantní v 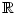 pro pro 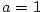 . .
|
Definice 3.25.
Buď 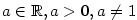 . Funkce inverzní k funkci . Funkce inverzní k funkci 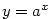 se nazývá
logaritmická funkce o základu se nazývá
logaritmická funkce o základu 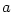 , značí se , značí se 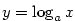 . .
|
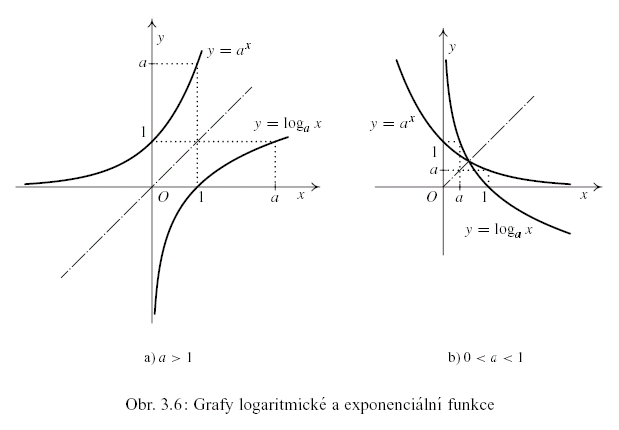
Z věty 3.24 vyplývá, že pro 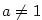 je exponenciální funkce je exponenciální funkce  ryze monotonní,
takže inverzní funkce skutečně existuje. Grafy jsou znázorněny na obr. 3.6 ryze monotonní,
takže inverzní funkce skutečně existuje. Grafy jsou znázorněny na obr. 3.6
Je-li  , nazývá se logaritmická funkce , nazývá se logaritmická funkce 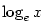 přirozený
logaritmus a značí se přirozený
logaritmus a značí se 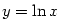 . .
Je-li 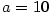 , nazývá se logaritmická funkce , nazývá se logaritmická funkce 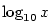 dekadický
logaritmus a značí se dekadický
logaritmus a značí se 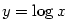 . .
3.5. Mocninná funkce
Definice 3.22 nám dovoluje zavést funkci 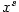 pro
libovolné reálné číslo pro
libovolné reálné číslo 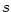 . .
Definice 3.28.
Buď 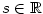 . Pro . Pro 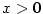 definujeme funkci definujeme funkci 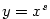 a nazýváme ji mocninnou funkcí.
a nazýváme ji mocninnou funkcí.
|
Věta 3.29.
Mocninná funkce 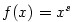 má tyto vlastnosti: má tyto vlastnosti:
-
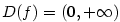 a a 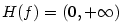 pro pro 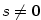 , , 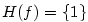 pro pro 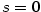 . .
- Funkce
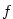 je rostoucí na je rostoucí na 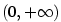 pro pro 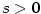 , klesající na , klesající na 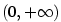 pro pro 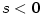 a konstantní na
a konstantní na 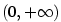 pro pro 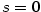 — viz obr. 3.7. — viz obr. 3.7.
- Platí
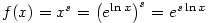 pro pro 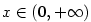 . .
|
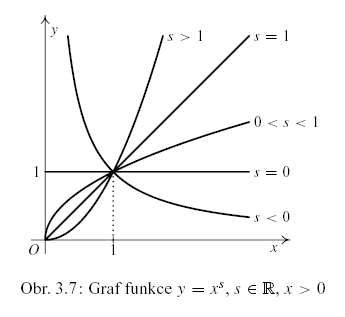
Poznámka 3.30.
V některých speciálních případech lze definiční obor 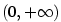 funkce funkce 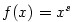 ještě
rozšířit. ještě
rozšířit.
- Je-li
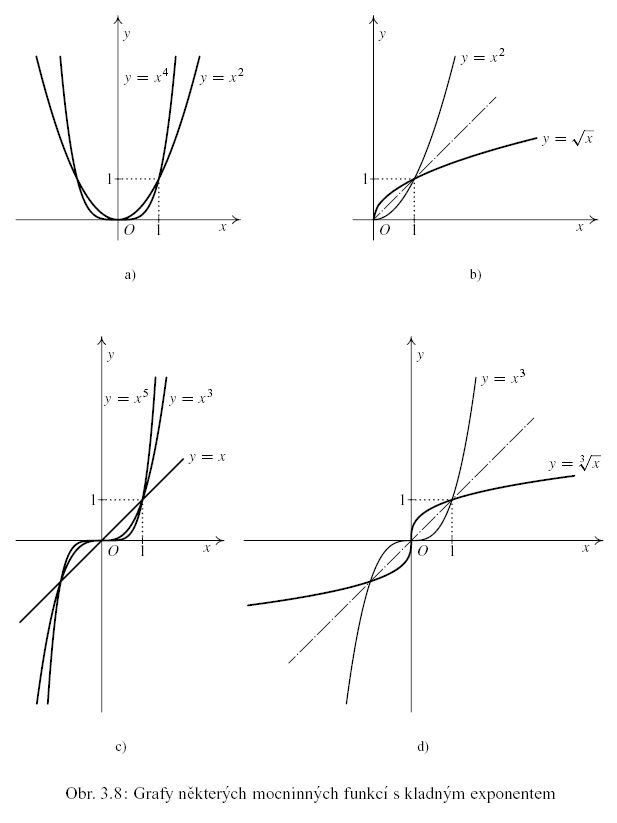
 , je , je  (např. (např.  , , 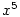 ) — viz obr. 3.8a) a 3.8c). ) — viz obr. 3.8a) a 3.8c).
- Je-li
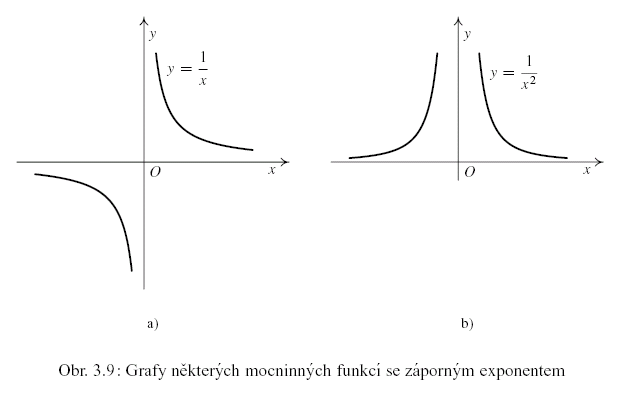
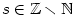 , je , je 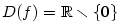 (např. (např. 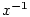 , , 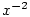 — viz obr. 3.9 — nebo
— viz obr. 3.9 — nebo 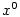 ). ).
- Je-li
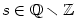 , kde , kde 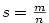 , , 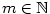 , , 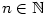 ,
je ,
je 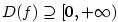 (např. (např. 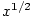 , , 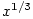 , , 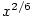 ). Viz též dále bod 5. ). Viz též dále bod 5.
-
Funkci
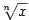 , kde , kde 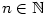 , , 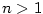 , chápeme jako inverzní funkci k mocnině , chápeme jako inverzní funkci k mocnině 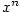 . .
-
V případě, že
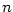 je sudé, není funkce je sudé, není funkce 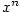 prostá na prostá na 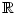 , ale je prostá na intervalu , ale je prostá na intervalu 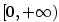 .
Tedy pro sudé .
Tedy pro sudé 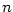 je funkce je funkce 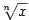 definovaná jen pro definovaná jen pro 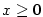 . .
-
V případě, že
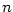 je liché, je funkce je liché, je funkce 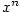 prostá na prostá na 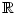 .
Tedy pro liché .
Tedy pro liché 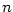 je funkce je funkce 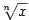 definovaná pro libovolné definovaná pro libovolné 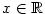 . .
Funkce 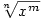 , kde , kde 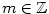 , , 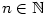 , je pak složenou funkcí
s vnitřní složkou , je pak složenou funkcí
s vnitřní složkou 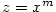 a s vnější složkou a s vnější složkou 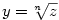 . Její definiční obor
závisí na konkrétních číslech . Její definiční obor
závisí na konkrétních číslech 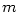 a a 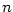 . .
- Obecně, je-li
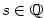 , definujeme , definujeme 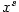 , kde , kde 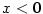 ,
právě když v základním tvaru ,
právě když v základním tvaru  čísla čísla 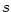 (tj.
(tj. 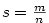 , , 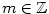 , , 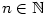 a čísla a čísla 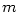 a a 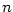 jsou nesoudělná)
je číslo jsou nesoudělná)
je číslo 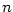 liché.
Pak klademe liché.
Pak klademe 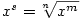 .
Tedy .
Tedy 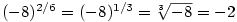 ,
zatímco ,
zatímco 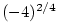 není definované, protože základní tvar zlomku není definované, protože základní tvar zlomku 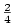 je je 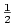 a číslo
a číslo 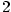 ve jmenovateli je sudé. Tato obecná definice je ve shodě s body 1 a 2. ve jmenovateli je sudé. Tato obecná definice je ve shodě s body 1 a 2.
Např. funkce
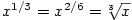 je definovaná pro je definovaná pro 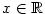 (viz obr. 3.8d)), kdežto
funkce (viz obr. 3.8d)), kdežto
funkce 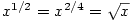 je definovaná jen pro je definovaná jen pro 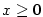 (viz obr. 3.8b)). (viz obr. 3.8b)).
- Dále si všimněme vztahu mezi funkcemi
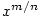 a a 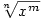 , kde , kde 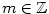 , ,
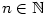 a a 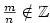 . .
-
Složená funkce
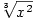 je definovaná pro je definovaná pro 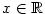 a platí a platí
 pro pro 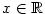 . .
-
Složená funkce
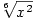 je definovaná
pro je definovaná
pro 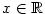 a platí a platí 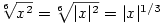 pro pro 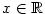 .
Tedy pro .
Tedy pro 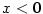 je je 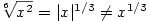 . .
-
Podobně musíme přistupovat k funkcím
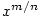 a a 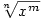 , kde , kde 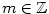 , ,
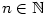 a a 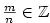 . Např. funkce . Např. funkce 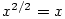 pro pro 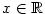 (podle bodu 1 resp. 5), zatímco
složená funkce (podle bodu 1 resp. 5), zatímco
složená funkce 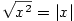 pro pro 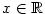 , jde tedy o dvě různé funkce se stejným definičním oborem,
jejichž hodnoty se shodují pouze pro , jde tedy o dvě různé funkce se stejným definičním oborem,
jejichž hodnoty se shodují pouze pro 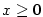 . .
Předchozí příklady ukazují, že je nutné respektovat
rozdíl mezi funkcemi 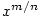 a a 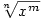 , , 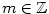 , , 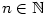 ,
chceme-li se vyhnout chybám. Např. zatímco funkce ,
chceme-li se vyhnout chybám. Např. zatímco funkce 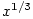 a a 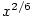 , , 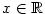 ,
jsou podle bodu 5 stejné, složené funkce ,
jsou podle bodu 5 stejné, složené funkce 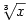 a a 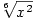 se shodují pro
se shodují pro 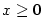 , avšak pro , avšak pro 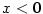 dávají různé hodnoty (funkce dávají různé hodnoty (funkce 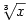 je lichá, kdežto funkce
je lichá, kdežto funkce 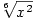 je sudá).
Poznamenejme, že v některých učebnicích se mocnina je sudá).
Poznamenejme, že v některých učebnicích se mocnina 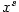 pro záporné pro záporné 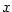 a necelé
a necelé 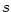 nezavádí. nezavádí.
|
Poznámka 3.31.
Při zavádění goniometrických funkcí jsme nepostupovali tak
exakt\-ně, jak to matematikové od poloviny 19. století vyžadují. Kvůli rozsahu celého
textu jsme také nedokazovali všechny uváděné vlastnosti elementárních funkcí.
Jiné, preciznější přístupy by vyžadovaly nejprve zavést pojmy jako limita,
spojitost a derivace. Nejčastějšími prostředky takových přístupů jsou mocninné řady
nebo funkcionální rovnice.
S různými variantami těchto pojetí je možné se seznámit např. v [15, 17, 21].
Pro první seznámení se základy
diferenciálního počtu je však tento přístup příliš náročný a zdlouhavý, a proto jsme vyšli
ze středoškolských znalostí a volili postup založený na jistém „přijatelném názoru”
zejména pokud jde o orientovaný úhel a délku oblouku kružnice.
Takový postup je ospravedlněný tím, že všechny zaváděné pojmy a o nich uváděná
tvrzení lze vybudovat bez tohoto názoru.
|
|
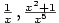 ; příkladem neryze lomené racionální funkce jsou funkce
; příkladem neryze lomené racionální funkce jsou funkce
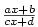 , kde
, kde 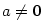 ,
, 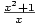 nebo
nebo  .
Platí následující tvrzení:
.
Platí následující tvrzení:
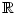 , napíšeme si formální tvar rozkladu na parciální zlomky
a určíme konstanty.
, napíšeme si formální tvar rozkladu na parciální zlomky
a určíme konstanty.
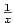 ,
a pak pomocí funkce k ní inverzní zavést funkci exponenciální, nebo definovat nejprve
funkci exponenciální a přes inverzi funkci logaritmickou. Protože první postup vyžaduje
znalosti základů integrálního počtu, z názorných důvodů
zvolíme druhý postup — zavedeme nejprve funkci exponenciální.
Ze střední školy je známo, jak definujeme mocninu
,
a pak pomocí funkce k ní inverzní zavést funkci exponenciální, nebo definovat nejprve
funkci exponenciální a přes inverzi funkci logaritmickou. Protože první postup vyžaduje
znalosti základů integrálního počtu, z názorných důvodů
zvolíme druhý postup — zavedeme nejprve funkci exponenciální.
Ze střední školy je známo, jak definujeme mocninu 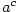 , kde
, kde
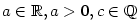 :
:
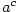 pro libovolné kladné reálné
pro libovolné kladné reálné 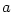 a
libovolné reálné
a
libovolné reálné  .
.
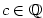 je tato nová definice ve shodě s původní. Rovněž je
možné dokázat pravidla pro počítání s mocninami, známá pro racionální exponenty.
Zejména platí (
je tato nová definice ve shodě s původní. Rovněž je
možné dokázat pravidla pro počítání s mocninami, známá pro racionální exponenty.
Zejména platí (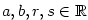 ,
, 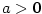 ,
, 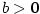 )
)
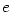 (Eulerovo
číslo — viz definice 2.27), tj. funkce
(Eulerovo
číslo — viz definice 2.27), tj. funkce 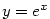 .
.
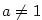 je exponenciální funkce
je exponenciální funkce  ryze monotonní,
takže inverzní funkce skutečně existuje. Grafy jsou znázorněny na obr. 3.6
ryze monotonní,
takže inverzní funkce skutečně existuje. Grafy jsou znázorněny na obr. 3.6
 , nazývá se logaritmická funkce
, nazývá se logaritmická funkce 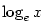 přirozený
logaritmus a značí se
přirozený
logaritmus a značí se 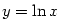 .
.
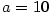 , nazývá se logaritmická funkce
, nazývá se logaritmická funkce 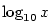 dekadický
logaritmus a značí se
dekadický
logaritmus a značí se 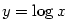 .
.
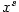 pro
libovolné reálné číslo
pro
libovolné reálné číslo 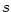 .
.