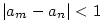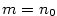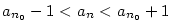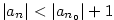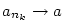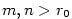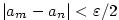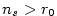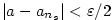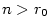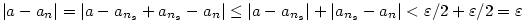Kapitola 2Posloupnosti
Důležitým speciálním případem funkce je posloupnost, tj. funkce definovaná na množině
přirozených čísel. Obsahem této kapitoly je pojem limita a obecnější pojem hromadné body posloupnosti.
Pomocí limity jisté posloupnosti budeme definovat Eulerovo číslo, které je důležité
pro zavedení elementárních funkcí.
2.1. Limita posloupnosti
Definice 2.1.
Posloupnost
je zobrazení 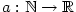 , jehož hodnoty obvykle místo , jehož hodnoty obvykle místo 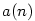 značíme značíme 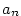 .
Hodnotu .
Hodnotu 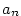 nazýváme nazýváme 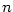 -tý člen posloupnosti a celou
posloupnost pak zapisujeme -tý člen posloupnosti a celou
posloupnost pak zapisujeme
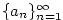 nebo nebo 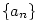 , příp. , příp. 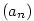 . .
|
Posloupnost je nejčastěji zadána buď výčtem členů, tj. 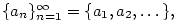 nebo rekurentním vzorcem, např.
nebo rekurentním vzorcem, např. 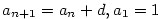 , nebo explicitním vzorcem pro , nebo explicitním vzorcem pro 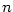 -tý člen,
např. -tý člen,
např. 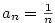 . .
Poznámka 2.2.
Posloupnost 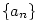 se nazývá se nazývá
rostoucí, jestliže 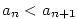 pro každé pro každé
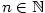 ;
klesající, jestliže ;
klesající, jestliže 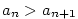 pro každé pro každé
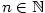 ;
nerostoucí, jestliže ;
nerostoucí, jestliže 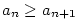 pro každé pro každé
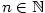 ;
neklesající, jestliže ;
neklesající, jestliže 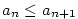 pro každé pro každé
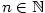 ;
shora ohraničená, jestliže existuje ;
shora ohraničená, jestliže existuje 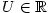 takové, že
takové, že 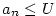 pro každé pro každé 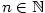 ;
zdola ohraničená, jestliže existuje ;
zdola ohraničená, jestliže existuje 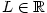 takové, že
takové, že 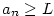 pro každé pro každé 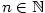 ;
ohraničená , jestliže
je ohraničená shora a i zdola. ;
ohraničená , jestliže
je ohraničená shora a i zdola.
|
Poznamenejme, že takto definované pojmy jsou ve shodě s definicemi 1.29 a
1.35 pro funkce 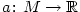 s obecnou množinou s obecnou množinou 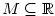 . .
Definice 2.3.
Nechť je dána posloupnost 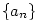 a číslo a číslo 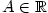 .
Řekneme, že posloupnost .
Řekneme, že posloupnost 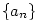 má limitu
má limitu 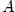 ,
jestliže ke každému ,
jestliže ke každému
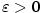 existuje existuje 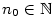 takové, že pro každé takové, že pro každé
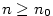 platí, že platí, že 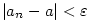 . Pomocí kvantifikátorů lze psát: . Pomocí kvantifikátorů lze psát:
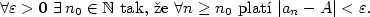
Pokud má posloupnost 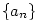 limitu, říkáme, že
konverguje, a značíme limitu, říkáme, že
konverguje, a značíme 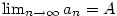 ,
případně ,
případně 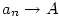 pro pro 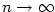 .
Řekneme, že posloupnost .
Řekneme, že posloupnost 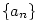 má limitu má limitu 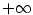 , jestliže
jestliže ke každému , jestliže
jestliže ke každému 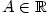 existuje existuje 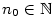 takové, že pro každé takové, že pro každé
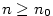 platí, že platí, že 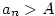 . Značíme . Značíme 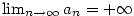 a pomocí kvantifikátorů zapisujeme
a pomocí kvantifikátorů zapisujeme
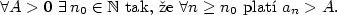
Podobně definujeme 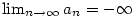 .
Pokud má posloupnost .
Pokud má posloupnost 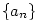 limitu limitu 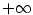 nebo nebo 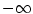 , říkáme, že posloupnost
diverguje. Jestliže posloupnost nekonverguje ani nediverguje, řekneme,
že osciluje. , říkáme, že posloupnost
diverguje. Jestliže posloupnost nekonverguje ani nediverguje, řekneme,
že osciluje.
|
Místo termínu posloupnost konverguje resp. diverguje říkáme též,
že posloupnost má vlastní limitu
resp. nevlastní limitu.

Poznámka 2.4. Platí
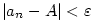 právě tehdy, když právě tehdy, když 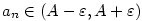 . .
|
| Věta 2.5.
Každá posloupnost má nejvýše jednu limitu.
|
Důkaz.
Větu dokážeme sporem. Nechť 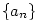 je
posloupnost a předpokládejme, že je
posloupnost a předpokládejme, že  , ,
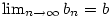 , , 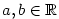 a a 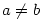 .
Bez újmy na obecnosti můžeme předpokládat, že .
Bez újmy na obecnosti můžeme předpokládat, že 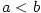 (pro (pro 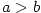 postupujeme
analogicky).
Zvolme postupujeme
analogicky).
Zvolme 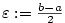 . Podle definice limity existují . Podle definice limity existují
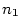 takové, že takové, že  platí platí 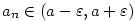 , ,
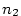 takové, že takové, že 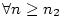 platí platí 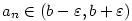 . .
Pro 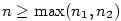 platí, že platí, že 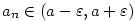 a současně a současně 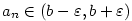 , což je
spor, protože tyto intervaly jsou disjunktní (tj. jejich průnik je prázdná množina).
Obdobně se vyšetří případy , což je
spor, protože tyto intervaly jsou disjunktní (tj. jejich průnik je prázdná množina).
Obdobně se vyšetří případy 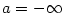 resp. resp. 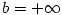 . .
|
Zobrazit / skrýt důkaz |
Příklad 2.6.
Dokažte z definice, že
a)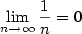 b)
b)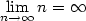
|
Zobrazit / skrýt řešení |
| Věta 2.7.
Každá konvergentní posloupnost je ohraničená.
|
Zobrazit / skrýt důkaz |
2.2. Věty o limitách
Věta 2.8.
Nechť 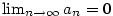 a posloupnost a posloupnost
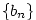 je ohraničená. Pak je ohraničená. Pak 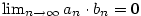 . .
|
Zobrazit / skrýt důkaz |
Příklad 2.9.
Vypočtěte 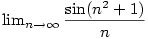 . .
|
Zobrazit / skrýt řešení |
Věta 2.10.
Nechť jsou dány posloupnosti  a existuje a existuje 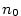 tak,
že pro každé tak,
že pro každé 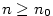 je je 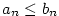 . Pak platí: . Pak platí:
- Jestliže
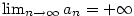 , pak i , pak i
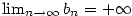 . .
- Jestliže
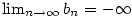 , pak i , pak i 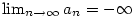 . .
|
Důkaz.
Důkaz provedeme pouze pro tvrzení 1 (druhé se dokáže
analogicky).
Nechť tedy 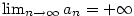 . Z definice limity k libovolnému . Z definice limity k libovolnému
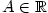 existuje existuje 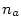 tak, že pro všechna tak, že pro všechna 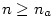 je je 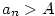 .
Navíc dle předpokladu existuje .
Navíc dle předpokladu existuje 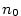 tak, že pro všechna tak, že pro všechna 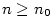 je je
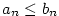 . Zvolme . Zvolme 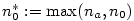 a vidíme, že pro všechna a vidíme, že pro všechna 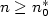 je je 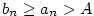 a tvrzení je dokázáno. a tvrzení je dokázáno.
|
Zobrazit / skrýt důkaz |
Věta 2.12.
Nechť jsou dány konvergentní posloupnosti  a a 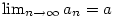 , , 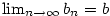 . Pak platí: . Pak platí:
- Jestliže
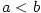 , pak existuje , pak existuje 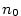 tak, že pro všechna tak, že pro všechna 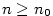 platí platí 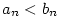 . .
- Jestliže existuje
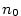 tak, že pro všechna tak, že pro všechna 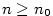 je je 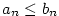 , pak , pak 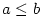 . .
|
Důkaz.
První tvrzení plyne snadno z definice limity. Druhé tvrzení plyne z prvního: Kdyby bylo 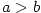 ,
pak by pro velká ,
pak by pro velká 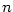 platilo platilo 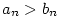 , což je spor. , což je spor.
|
Zobrazit / skrýt důkaz |
I když bude v druhém tvrzení předchozí věty platit 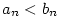 , může být , může být 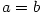 , jak ukazuje
příklad posloupností , jak ukazuje
příklad posloupností 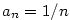 , , 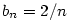 , kdy , kdy 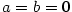 . .
Věta 2.13.
Nechť jsou dány posloupnosti  a a 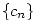 a číslo a číslo 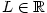 takové, že takové, že
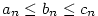 pro všechna pro všechna 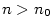 , a , a
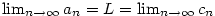 . Pak také . Pak také 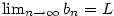 . .
|
Zobrazit / skrýt důkaz |
Příklad 2.14.
Určete 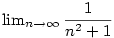 . .
|
Zobrazit / skrýt řešení |
Věta 2.15.
Nechť 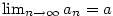 a a 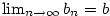 , kde , kde 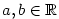 . Pak platí: . Pak platí:
-
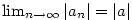 . .
-
 . .
-
 . .
- Pokud
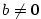 , pak , pak
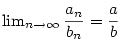 . .
|
Důkaz.
- Podle předpokladu platí
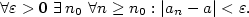
Z vlastností absolutní hodnoty plyne: 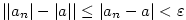 a tvrzení je dokázáno. a tvrzení je dokázáno.
-
Chceme ukázat, že ke každému
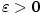 existuje existuje 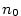 takové, že pro
všechna takové, že pro
všechna 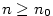 je je 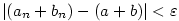 . Dle předpokladů
existuje pro nějaké . Dle předpokladů
existuje pro nějaké  (určíme je později) (určíme je později)
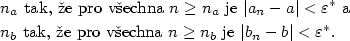
Zvolme 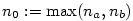 a a
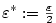 . Vidíme,
že pro všechna . Vidíme,
že pro všechna  je : je :
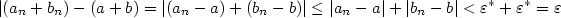
a tvrzení je dokázáno.
- Postupujeme obdobně jako v případě 2, opět k nějakému
 najdeme najdeme  požadovaných vlastností. Dále podle věty
2.7 existuje požadovaných vlastností. Dále podle věty
2.7 existuje 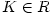 tak, že tak, že 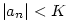 pro všechna pro všechna 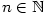 . Upravujme: . Upravujme:
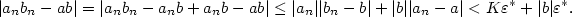
Vidíme, že když zvolíme 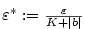 , je
tvrzení dokázáno. , je
tvrzení dokázáno.
-
Protože
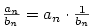 , stačí dokázat, že , stačí dokázat, že
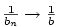 , zbytek plyne z předchozího tvrzení.
Nejprve provedeme úpravu , zbytek plyne z předchozího tvrzení.
Nejprve provedeme úpravu
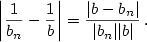
Podle tvrzení 1 platí 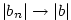 a podle
věty 2.12
existuje a podle
věty 2.12
existuje 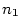 tak, že pro všechna tak, že pro všechna 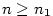 je je 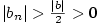 .
Obdobně jako v předchozích tvrzeních existuje k nějakému .
Obdobně jako v předchozích tvrzeních existuje k nějakému  index
index 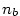 tak, že pro všechna tak, že pro všechna 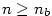 je je 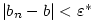 . Zvolme . Zvolme
 . Pak pro všechna . Pak pro všechna 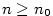 platí platí
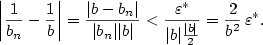
Stačí tedy zvolit 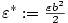 a tvrzení je
dokázáno. a tvrzení je
dokázáno.
|
Zobrazit / skrýt důkaz |
Příklad 2.17.
Určete
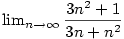 . .
|
| Řešení. Podle Věty 2.15 platí
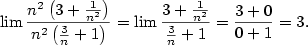
|
Zobrazit / skrýt řešení |
Věta 2.18.
Nechť je dána posloupnost 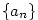 . .
- Jestliže
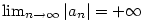 , pak , pak 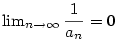 (heslo
(heslo 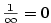 ). ).
- Jestliže
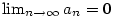 a existuje a existuje 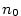 takové, že pro všechna takové, že pro všechna 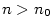 je je 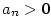 , pak , pak
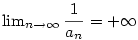 (heslo (heslo 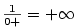 ).
Analogicky platí tvrzení vystižené heslem ).
Analogicky platí tvrzení vystižené heslem 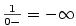 . .
|
Důkaz.
-
Buď
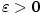 .
Chceme ukázat, že
existuje .
Chceme ukázat, že
existuje 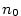 takové, že pro všechna takové, že pro všechna 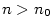 je
je 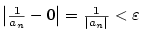 .
Z existence limity .
Z existence limity 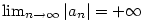 plyne, že k číslu plyne, že k číslu 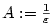 existuje
existuje 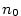 tak, že všechna tak, že všechna 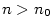 platí platí 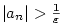 .
Pak pro .
Pak pro 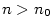 platí platí 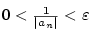 a tvrzení je dokázáno. a tvrzení je dokázáno.
-
Buď
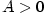 .
Chceme dokázat, že
existuje .
Chceme dokázat, že
existuje 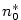 takové, že pro všechna takové, že pro všechna 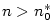 je je
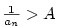 . Podle předpokladu platí . Podle předpokladu platí 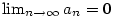 .
Proto k číslu .
Proto k číslu 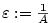 existuje existuje
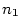 takové, že pro všechna takové, že pro všechna  je je 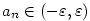 .
Zvolme .
Zvolme
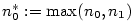 . Pak pro . Pak pro 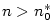 je je
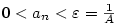 , odkud , odkud 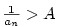 . Tvrzení je dokázáno. . Tvrzení je dokázáno.
|
Zobrazit / skrýt důkaz |
Věta 2.20.
Každá neklesající shora ohraničená posloupnost 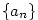 má vlastní limitu. Přitom platí má vlastní limitu. Přitom platí
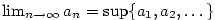 . .
Podobně každá nerostoucí zdola ohraničená posloupnost 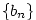 má vlastní limitu
a platí má vlastní limitu
a platí 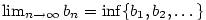 . .
|
Důkaz.
Dokážeme pouze první tvrzení, důkaz druhého se provede analogicky.
Nechť 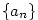 je neklesající posloupnost shora ohraničená.
Podle axiomu R13 má každá neprázdná shora ohraničená množina supremum.
Označíme tudíž je neklesající posloupnost shora ohraničená.
Podle axiomu R13 má každá neprázdná shora ohraničená množina supremum.
Označíme tudíž 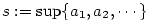 , , 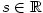 , a dokážeme, že , a dokážeme, že
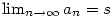 . .
Z druhé vlastnosti suprema plyne, že
pro každé 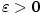 existuje existuje 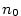 takové, že takové, že
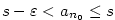 . Posloupnost . Posloupnost 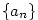 je neklesající,
proto pro každé je neklesající,
proto pro každé
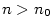 je je 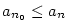 . Odtud . Odtud
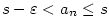 , neboli , neboli  . Tvrzení je dokázáno. . Tvrzení je dokázáno.
|
Zobrazit / skrýt důkaz |
| Příklad 2.21.
Vypočtete limitu
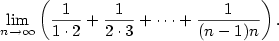
|
Řešení.
Nejprve si uvědomíme, že platí 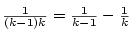 (ověřte sami). Potom (ověřte sami). Potom
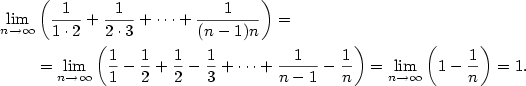
|
Zobrazit / skrýt řešení |
| Příklad 2.22.
Vypočtete
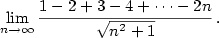
|
| Řešení.
Podle vzorce pro součet členů aritmetické posloupnosti je
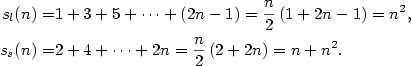
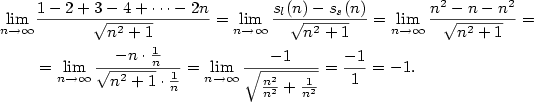
|
Zobrazit / skrýt řešení |
Příklad 2.23.
Vypočtěte 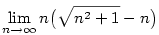 . .
|
| Řešení. Máme
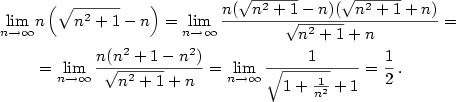
|
Zobrazit / skrýt řešení |
| Příklad 2.24.
Vypočtěte
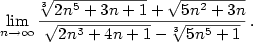
|
| Řešení.
Vytkneme z každé odmocniny člen v nejvyšší mocnině
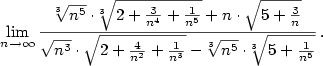
Zkrátíme zlomek výrazem 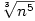 a dostaneme a dostaneme
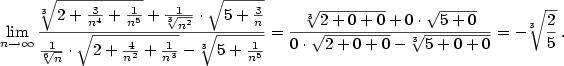
|
Zobrazit / skrýt řešení |
Příklad 2.25.
Vypočtěte 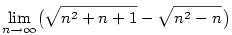 . .
|
| Řešení.
Postupujeme obdobně jako v příkladě 2.23:
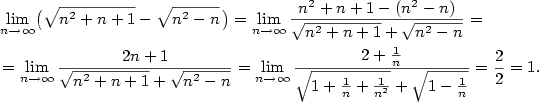
|
Zobrazit / skrýt řešení |
2.3. Eulerovo číslo
Věta 2.26.
Posloupnost  , kde , kde 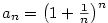 , je rostoucí a shora ohraničená,
posloupnost , je rostoucí a shora ohraničená,
posloupnost 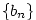 , kde , kde 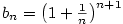 , je klesající a zdola ohraničená,
jsou tedy obě konvergentní. Mají tutéž limitu. , je klesající a zdola ohraničená,
jsou tedy obě konvergentní. Mají tutéž limitu.
|
Zobrazit / skrýt důkaz |
Společná limita obou posloupností z předchozího příkladu má velký význam.
Definice 2.27.
Limitu 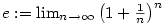 nazýváme Eulerovo
číslo. nazýváme Eulerovo
číslo.
|
Poznámka 2.28.
O číslu  lze dokázat, že je iracionální --- viz např. [7, str. 81], [17, str. 181]
nebo [21, str. 89]; rovněž číslo lze dokázat, že je iracionální --- viz např. [7, str. 81], [17, str. 181]
nebo [21, str. 89]; rovněž číslo 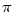 je iracionální --- viz [15, str. 183]. je iracionální --- viz [15, str. 183].
Číslo se nazývá algebraické, je-li kořenem nějakého nenulového
polynomu s celočíselnými koeficienty. Mezi tato čísla patří všechna racionální čísla.
Příkladem iracionálních algebraických čísel je třeba 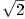 , , 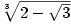 a pod.
Zbývající reálná čísla se nazývají transcendentní.
Číslo a pod.
Zbývající reálná čísla se nazývají transcendentní.
Číslo  je transcendentní --- viz [8, str. 147].
Také číslo je transcendentní --- viz [8, str. 147].
Také číslo 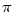 je transcendentní --- viz [18, str. 205]. Srovnejte též
příklad D43 dodatku. je transcendentní --- viz [18, str. 205]. Srovnejte též
příklad D43 dodatku.
|
| Příklad 2.29.
Vypočtěte
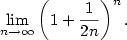
|
Zobrazit / skrýt řešení |
2.4. Hromadné body posloupnosti
Definice 2.30.
Nechť 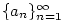 je posloupnost a nechť je posloupnost a nechť 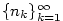 je rostoucí posloupnost
přirozených čísel. Pak posloupnost je rostoucí posloupnost
přirozených čísel. Pak posloupnost 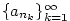 se nazývá vybraná posloupnost
(podposloupnost) z posloupnosti se nazývá vybraná posloupnost
(podposloupnost) z posloupnosti 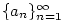 . .
|
Příklad 2.31.
Najděte všechny konvergentní podposloupnosti posloupnosti 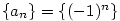 . .
|
Zobrazit / skrýt řešení |
Věta 2.32.
Nechť 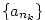 je vybraná posloupnost z posloupnosti je vybraná posloupnost z posloupnosti 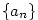 a a 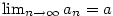 .
Potom .
Potom  . .
|
Důkaz.
Tvrzení dokážeme přímo z definice limity. Nechť je dáno libovolné 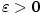 .
Pak podle předpokladu
existuje .
Pak podle předpokladu
existuje 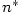 takové, že pro všechna takové, že pro všechna 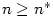 je je
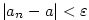 . Posloupnost . Posloupnost 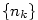 je rostoucí posloupnost
přirozených čísel, proto můžeme zvolit je rostoucí posloupnost
přirozených čísel, proto můžeme zvolit 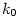 tak, že tak, že 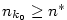 . Pak
pro všechna . Pak
pro všechna 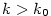 je je 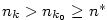 , a proto platí , a proto platí
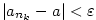 . Tvrzení je dokázáno. . Tvrzení je dokázáno.
|
Zobrazit / skrýt důkaz |
Předchozí věta se někdy užívá pro důkaz neexistence limity dané
posloupnosti. Ukažme si to na jednoduché posloupnosti
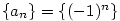 z příkladu 2.31. Kdyby existovala limita z příkladu 2.31. Kdyby existovala limita
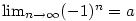 , pak by toto číslo bylo limitou i
každé vybrané posloupnosti, a proto by muselo platit, že , pak by toto číslo bylo limitou i
každé vybrané posloupnosti, a proto by muselo platit, že
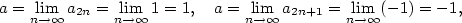
což je evidentní spor, a tedy daná posloupnost 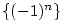 nemá limitu.
Pro posloupnosti, které nejsou konvergentní, je důležitý pojem hromadného bodu
zobecňující pojem limity posloupnosti. nemá limitu.
Pro posloupnosti, které nejsou konvergentní, je důležitý pojem hromadného bodu
zobecňující pojem limity posloupnosti.
Definice 2.33.
Číslo 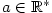 se nazývá hromadný bod posloupnosti se nazývá hromadný bod posloupnosti 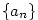 , jestliže
pro každé okolí , jestliže
pro každé okolí 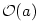 existuje nekonečně mnoho indexů existuje nekonečně mnoho indexů 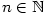 , pro které platí, že , pro které platí, že
 . .
|
Věta 2.34.
Číslo  je hromadným bodem posloupnosti je hromadným bodem posloupnosti 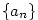 právě tehdy, když
existuje vybraná podposloupnost právě tehdy, když
existuje vybraná podposloupnost
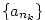 taková, že taková, že 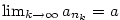 . .
|
| Důkaz.
Tvrzení snadno plyne přímo z definice hromadného bodu a vybrané
posloupnosti.
|
Zobrazit / skrýt důkaz |
Příklad 2.35.
Najděte všechny hromadné body posloupnosti 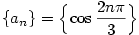 . .
|
Zobrazit / skrýt řešení |
| Lemma 2.36.
Každá posloupnost má nejmenší a největší hromadný bod.
|
Důkaz.
Důkaz tohoto intuitivně zřejmého tvrzení je následující.
Nechť je posloupnost 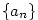 ohraničená. Definujme dvě pomocné posloupnosti ohraničená. Definujme dvě pomocné posloupnosti
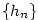 a a 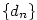 následovně: následovně: 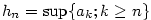 a a 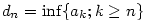 , , 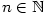 .
Zřejmě platí .
Zřejmě platí 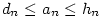 . Dále posloupnost . Dále posloupnost 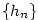 je nerostoucí a posloupnost je nerostoucí a posloupnost 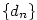 je neklesající. Obě jsou ohraničené. Podle věty 2.20 existují tedy
je neklesající. Obě jsou ohraničené. Podle věty 2.20 existují tedy
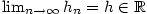 a
a 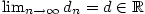 , přičemž , přičemž 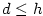 podle věty podle 2.12, 2. podle věty podle 2.12, 2.
Ukážeme, že 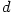 a a 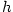 jsou hromadné body posloupnosti jsou hromadné body posloupnosti 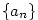 .
Ověříme to např. pro .
Ověříme to např. pro 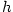 .
Z definice suprema plyne, že ke každému .
Z definice suprema plyne, že ke každému 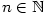 existuje index existuje index 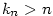 takový, že platí nerovnost takový, že platí nerovnost
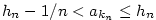 . Přitom lze předpokládat (po případném přechodu k podposloupnosti),
že posloupnost . Přitom lze předpokládat (po případném přechodu k podposloupnosti),
že posloupnost 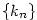 je rostoucí.
Z věty 2.13 nyní plyne, že je rostoucí.
Z věty 2.13 nyní plyne, že 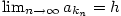 .
Existuje tudíž vybraná podposloupnost, která má za limitu .
Existuje tudíž vybraná podposloupnost, která má za limitu 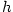 . .
Dále ukážeme, že pro libovolný hromadný bod  posloupnosti posloupnosti 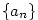 je je 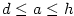 . Existuje
totiž vybraná konvergentní podposloupnost . Existuje
totiž vybraná konvergentní podposloupnost 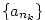 , pro niž , pro niž 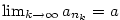 .
Pak platí nerovnost .
Pak platí nerovnost 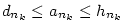 , z čehož podle věty 2.12, 2 plyne tvrzení.
Tedy , z čehož podle věty 2.12, 2 plyne tvrzení.
Tedy 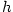 je největší a je největší a 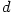 je nejmenší hromadný bod posloupnosti je nejmenší hromadný bod posloupnosti 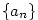 . .
Nyní vyšetříme neohraničené posloupnosti.
Je-li posloupnost 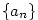 shora resp. zdola neohraničená, ukážeme, že shora resp. zdola neohraničená, ukážeme, že
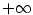 resp. resp. 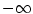 je její hromadný bod. je její hromadný bod.
Nechť je 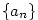 posloupnost shora neohraničená, tj. pro každé posloupnost shora neohraničená, tj. pro každé
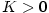 existuje existuje 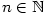 takové, že takové, že 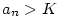 .
Indukcí můžeme sestrojit rostoucí posloupnost indexů .
Indukcí můžeme sestrojit rostoucí posloupnost indexů 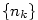 takovou, že takovou, že
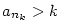 pro všechna pro všechna 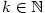 . Pak zřejmě podle věty 2.10, 1 je . Pak zřejmě podle věty 2.10, 1 je
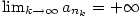 , proto je podle věty 2.34
také , proto je podle věty 2.34
také 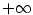 hromadným bodem posloupnosti hromadným bodem posloupnosti 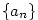 . .
Analogicky bychom vyšetřili případ zdola neohraničené posloupnosti; v tomto
případě pak je 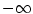 hromadným bodem posloupnosti. hromadným bodem posloupnosti.
Konečně si všimneme, že posloupnost 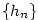 lze definovat pro libovolnou shora ohraničenou
posloupnost (pak ovšem může být i lze definovat pro libovolnou shora ohraničenou
posloupnost (pak ovšem může být i 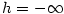 ; příkladem je posloupnost ; příkladem je posloupnost 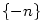 )
a posloupnost )
a posloupnost 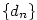 lze definovat pro libovolnou zdola ohraničenou posloupnost
(pak ovšem může být i lze definovat pro libovolnou zdola ohraničenou posloupnost
(pak ovšem může být i 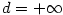 ; příkladem je posloupnost ; příkladem je posloupnost 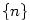 ). Přitom bude platit ). Přitom bude platit
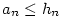 resp. resp. 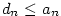 . Je-li např. . Je-li např. 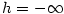 , je vzhledem k nerovnosti , je vzhledem k nerovnosti 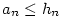 podle věty 2.10, 2 také
podle věty 2.10, 2 také 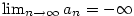 . Podobně se postupuje v případě . Podobně se postupuje v případě
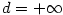 . .
Tedy ve všech případech existuje největší a nejmenší hromadný bod.
|
Zobrazit / skrýt důkaz |
Poznámka 2.37.
Posloupnosti 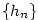 a a 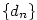 z předchozího důkazu je možné zavést dokonce
pro libovolnou posloupnost,
pokud pro shora (resp. zdola) neohraničené posloupnosti položíme z předchozího důkazu je možné zavést dokonce
pro libovolnou posloupnost,
pokud pro shora (resp. zdola) neohraničené posloupnosti položíme 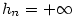 (resp. (resp. 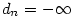 )
pro každé )
pro každé 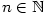 . Pak klademe . Pak klademe 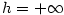 (resp. (resp. 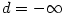 ). ).
|
Ilustrujme konstrukci z předchozího důkazu na příkladech.
- Pro
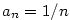 je je 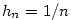 , ,  , , 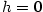 a a 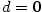 . .
- Pro
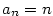 je je 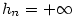 , , 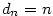 , , 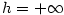 a a 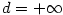 . .
- Pro
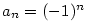 je je 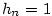 , , 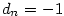 , , 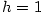 a a 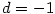 . .
- Pro
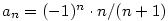 je je 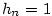 , , 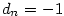 , , 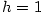 a a 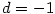 . .
| Důsledek 2.38.
Každá posloupnost má alespoň jeden hromadný bod.
|
Následující věta má velký význam v řadě partií matematické analýzy. Její důkaz bezprostředně
vyplývá z lemmatu 2.36.
| Věta 2.39. [Bolzanova-Weierstrassova]
Z každé ohraničené posloupnosti lze vybrat konvergentní podposloupnost.
|
Definice 2.40.
Nechť je dána posloupnost 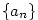 . Pak největší hromadný bod této
posloupnosti nazveme limita superior a označujeme . Pak největší hromadný bod této
posloupnosti nazveme limita superior a označujeme
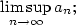
nejmenší hromadný bod této posloupnosti nazveme limita inferior
a označujeme
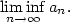
|
Příklad 2.41.
Vypočtěte 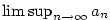 a a  posloupnosti posloupnosti
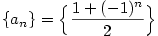 . .
|
Zobrazit / skrýt řešení |
Z předchozího snadno plyne následující důležitá věta.
Věta 2.42.
Posloupnost 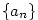 má limitu právě tehdy, když má limitu právě tehdy, když
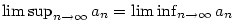 .
Všechny tři hodnoty jsou pak stejné. .
Všechny tři hodnoty jsou pak stejné.
|
Důkaz.
„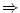 ”
Existuje-li ”
Existuje-li 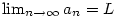 , pak každá vybraná podposloupnost má tutéž limitu , pak každá vybraná podposloupnost má tutéž limitu 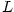 .
Posloupnost má proto jediný hromadný bod .
Posloupnost má proto jediný hromadný bod 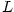 , takže její limita superior a limita inferior se musí rovnat. , takže její limita superior a limita inferior se musí rovnat.
„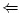 ”
Označme ”
Označme 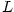 společnou hodnotu limity superior a limity inferior. Nechť nejprve společnou hodnotu limity superior a limity inferior. Nechť nejprve 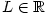 .
K libovolnému .
K libovolnému 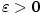 lze najít index lze najít index 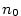 tak, že pro tak, že pro 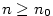 je je
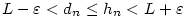 . Protože platí . Protože platí 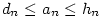 , je , je
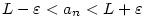 kdykoliv kdykoliv 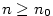 , tedy limita posloupnosti , tedy limita posloupnosti 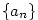 existuje a je rovna
existuje a je rovna 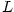 . Podobně se vyšetří případy . Podobně se vyšetří případy 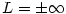 . .
|
Zobrazit / skrýt důkaz |
Následující tvrzení bývá často nazýváno
Bolzanovo-Cauchyovo kritérium. Má
především teoretický význam v důkazech existence limit.
Místo cauchyovská posloupnost se také používá název
fundamentální posloupnost.
Obsah věty 2.43 pak vyjadřujeme termínem, že množina 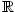 je úplná. Vlastnost úplnosti
doplněná o archimedovskost je ve skutečnosti ekvivalentní axiomu R13
z definice 1.8 a je významnou vlastností reálných čísel - viz dodatek, věta D14.
Dodejme, že např. množina
je úplná. Vlastnost úplnosti
doplněná o archimedovskost je ve skutečnosti ekvivalentní axiomu R13
z definice 1.8 a je významnou vlastností reálných čísel - viz dodatek, věta D14.
Dodejme, že např. množina 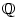 úplná není.} úplná není.}
|
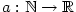 , jehož hodnoty obvykle místo
, jehož hodnoty obvykle místo 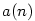 značíme
značíme 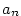 .
Hodnotu
.
Hodnotu 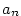 nazýváme
nazýváme 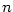 -tý člen posloupnosti a celou
posloupnost pak zapisujeme
-tý člen posloupnosti a celou
posloupnost pak zapisujeme
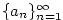 nebo
nebo 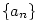 , příp.
, příp. 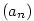 .
.
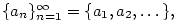 nebo rekurentním vzorcem, např.
nebo rekurentním vzorcem, např. 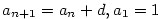 , nebo explicitním vzorcem pro
, nebo explicitním vzorcem pro 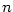 -tý člen,
např.
-tý člen,
např. 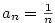 .
.
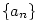 se nazývá
se nazývá
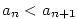 pro každé
pro každé
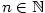 ;
klesající, jestliže
;
klesající, jestliže 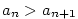 pro každé
pro každé
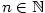 ;
nerostoucí, jestliže
;
nerostoucí, jestliže 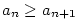 pro každé
pro každé
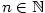 ;
neklesající, jestliže
;
neklesající, jestliže 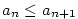 pro každé
pro každé
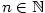 ;
shora ohraničená, jestliže existuje
;
shora ohraničená, jestliže existuje 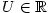 takové, že
takové, že 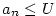 pro každé
pro každé 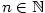 ;
zdola ohraničená, jestliže existuje
;
zdola ohraničená, jestliže existuje 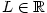 takové, že
takové, že 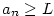 pro každé
pro každé 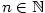 ;
ohraničená , jestliže
je ohraničená shora a i zdola.
;
ohraničená , jestliže
je ohraničená shora a i zdola.
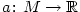 s obecnou množinou
s obecnou množinou 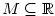 .
.
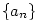 a číslo
a číslo 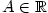 .
Řekneme, že posloupnost
.
Řekneme, že posloupnost 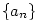 má limitu
má limitu 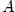 ,
jestliže ke každému
,
jestliže ke každému
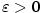 existuje
existuje 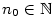 takové, že pro každé
takové, že pro každé
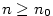 platí, že
platí, že 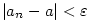 . Pomocí kvantifikátorů lze psát:
. Pomocí kvantifikátorů lze psát:
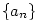 limitu, říkáme, že
konverguje, a značíme
limitu, říkáme, že
konverguje, a značíme 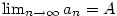 ,
případně
,
případně 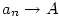 pro
pro 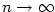 .
Řekneme, že posloupnost
.
Řekneme, že posloupnost 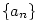 má limitu
má limitu 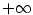 , jestliže
jestliže ke každému
, jestliže
jestliže ke každému 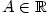 existuje
existuje 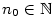 takové, že pro každé
takové, že pro každé
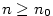 platí, že
platí, že 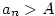 . Značíme
. Značíme 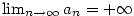 a pomocí kvantifikátorů zapisujeme
a pomocí kvantifikátorů zapisujeme
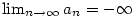 .
Pokud má posloupnost
.
Pokud má posloupnost 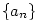 limitu
limitu 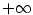 nebo
nebo 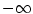 , říkáme, že posloupnost
diverguje. Jestliže posloupnost nekonverguje ani nediverguje, řekneme,
že osciluje.
, říkáme, že posloupnost
diverguje. Jestliže posloupnost nekonverguje ani nediverguje, řekneme,
že osciluje.

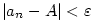 právě tehdy, když
právě tehdy, když 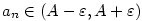 .
.
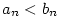 , může být
, může být 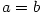 , jak ukazuje
příklad posloupností
, jak ukazuje
příklad posloupností 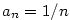 ,
, 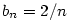 , kdy
, kdy 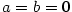 .
.
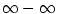 ”,
”,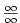 ,
,
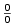 limita může existovat, ale nemusí.
limita může existovat, ale nemusí.
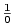 mohou nastat tři případy:
limita je
mohou nastat tři případy:
limita je 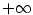 ,
, 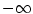 nebo limita neexistuje.
Jako ilustraci uveďme
nebo limita neexistuje.
Jako ilustraci uveďme
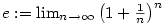 nazýváme Eulerovo
číslo.
nazýváme Eulerovo
číslo.
 lze dokázat, že je iracionální --- viz např. [7, str. 81], [17, str. 181]
nebo [21, str. 89]; rovněž číslo
lze dokázat, že je iracionální --- viz např. [7, str. 81], [17, str. 181]
nebo [21, str. 89]; rovněž číslo 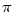 je iracionální --- viz [15, str. 183].
je iracionální --- viz [15, str. 183].
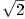 ,
, 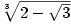 a pod.
Zbývající reálná čísla se nazývají transcendentní.
Číslo
a pod.
Zbývající reálná čísla se nazývají transcendentní.
Číslo  je transcendentní --- viz [8, str. 147].
Také číslo
je transcendentní --- viz [8, str. 147].
Také číslo 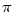 je transcendentní --- viz [18, str. 205]. Srovnejte též
příklad D43 dodatku.
je transcendentní --- viz [18, str. 205]. Srovnejte též
příklad D43 dodatku.
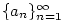 je posloupnost a nechť
je posloupnost a nechť 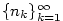 je rostoucí posloupnost
přirozených čísel. Pak posloupnost
je rostoucí posloupnost
přirozených čísel. Pak posloupnost 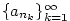 se nazývá vybraná posloupnost
(podposloupnost) z posloupnosti
se nazývá vybraná posloupnost
(podposloupnost) z posloupnosti 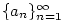 .
.
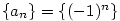 z příkladu 2.31. Kdyby existovala limita
z příkladu 2.31. Kdyby existovala limita
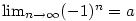 , pak by toto číslo bylo limitou i
každé vybrané posloupnosti, a proto by muselo platit, že
, pak by toto číslo bylo limitou i
každé vybrané posloupnosti, a proto by muselo platit, že
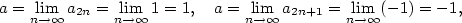
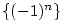 nemá limitu.
Pro posloupnosti, které nejsou konvergentní, je důležitý pojem hromadného bodu
zobecňující pojem limity posloupnosti.
nemá limitu.
Pro posloupnosti, které nejsou konvergentní, je důležitý pojem hromadného bodu
zobecňující pojem limity posloupnosti.
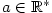 se nazývá hromadný bod posloupnosti
se nazývá hromadný bod posloupnosti 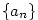 , jestliže
pro každé okolí
, jestliže
pro každé okolí 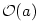 existuje nekonečně mnoho indexů
existuje nekonečně mnoho indexů 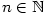 , pro které platí, že
, pro které platí, že
 .
.
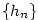 a
a 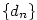 z předchozího důkazu je možné zavést dokonce
pro libovolnou posloupnost,
pokud pro shora (resp. zdola) neohraničené posloupnosti položíme
z předchozího důkazu je možné zavést dokonce
pro libovolnou posloupnost,
pokud pro shora (resp. zdola) neohraničené posloupnosti položíme 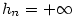 (resp.
(resp. 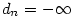 )
pro každé
)
pro každé 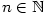 . Pak klademe
. Pak klademe 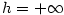 (resp.
(resp. 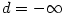 ).
).
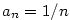 je
je 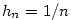 ,
,  ,
, 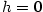 a
a 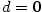 .
.
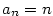 je
je 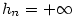 ,
, 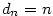 ,
, 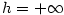 a
a 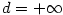 .
.
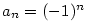 je
je 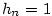 ,
, 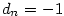 ,
, 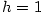 a
a 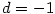 .
.
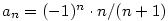 je
je 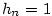 ,
, 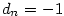 ,
, 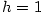 a
a 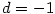 .
.
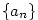 . Pak největší hromadný bod této
posloupnosti nazveme limita superior a označujeme
. Pak největší hromadný bod této
posloupnosti nazveme limita superior a označujeme
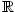 je úplná. Vlastnost úplnosti
doplněná o archimedovskost je ve skutečnosti ekvivalentní axiomu R13
z definice 1.8 a je významnou vlastností reálných čísel - viz dodatek, věta D14.
Dodejme, že např. množina
je úplná. Vlastnost úplnosti
doplněná o archimedovskost je ve skutečnosti ekvivalentní axiomu R13
z definice 1.8 a je významnou vlastností reálných čísel - viz dodatek, věta D14.
Dodejme, že např. množina 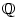 úplná není.}
úplná není.}
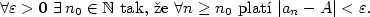
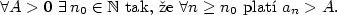

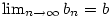
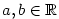
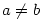
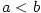
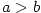
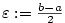
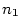

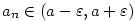
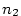
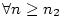
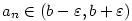
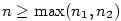
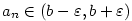
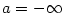
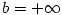
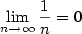 b)
b)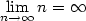
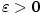
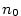
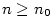
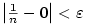
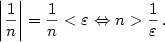
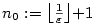
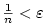
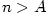
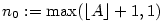
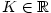
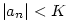
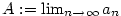
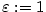
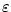
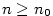

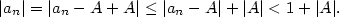
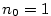
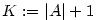
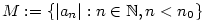
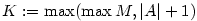
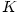
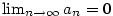
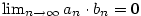
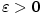

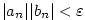
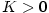
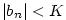

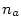
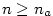
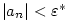
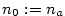
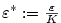
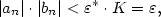
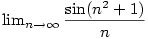
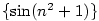
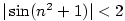
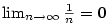
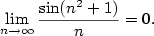

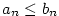
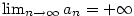
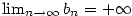
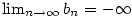
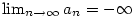
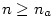
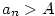
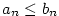
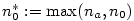
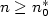
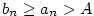
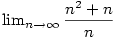
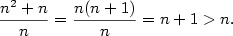
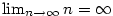
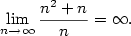
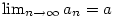
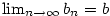
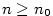
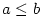
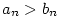
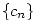
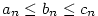
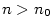
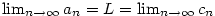
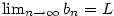
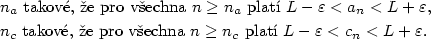
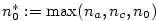
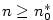
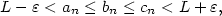
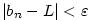
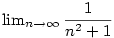
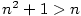
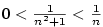
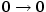
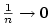
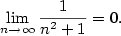
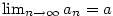
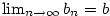
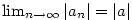


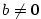
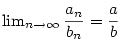
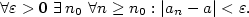
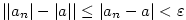
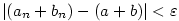
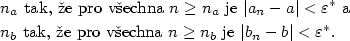
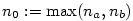
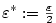
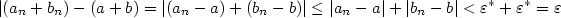
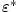
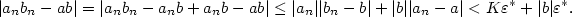
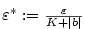
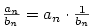
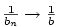
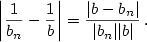
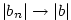
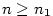
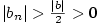
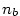
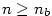
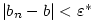

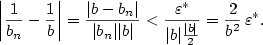
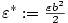
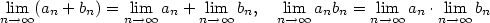
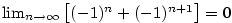
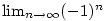
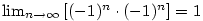
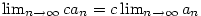
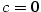
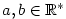
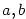
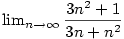
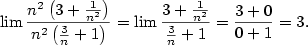
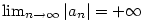
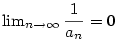
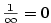
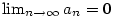
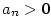
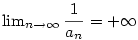
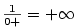
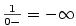
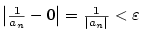
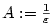
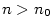
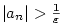
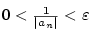
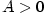
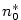
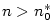
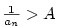
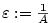

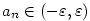
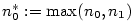
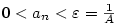
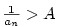
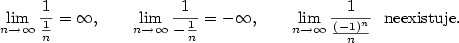
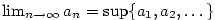
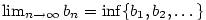
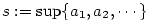
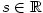
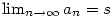
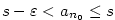
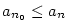
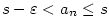

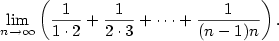
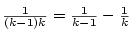
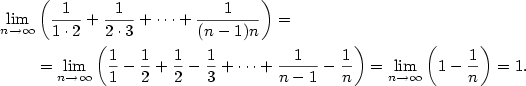
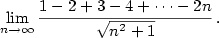
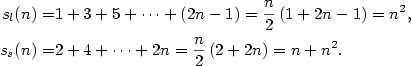
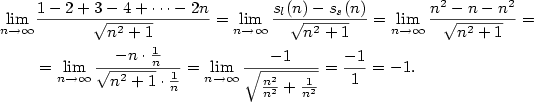
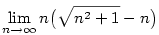
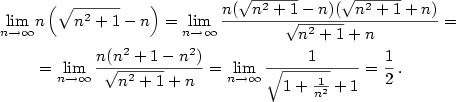
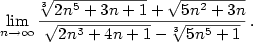
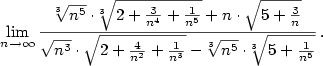
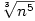
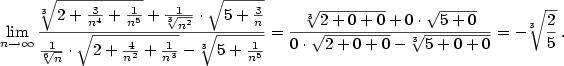
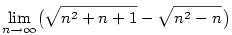
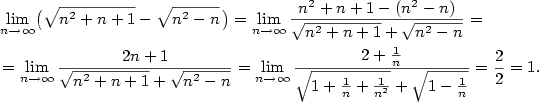
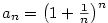
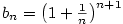
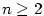
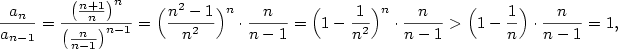
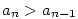
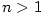
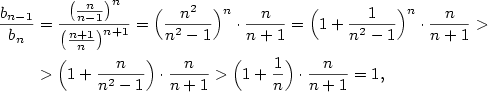
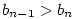
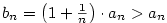
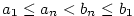
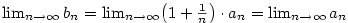
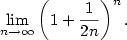
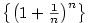
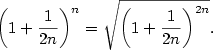

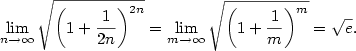
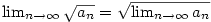
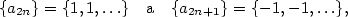
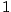
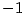
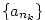
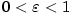
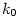
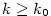
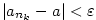

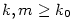
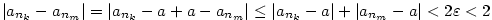
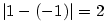
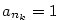

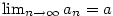

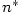
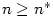
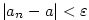
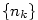
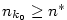
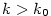
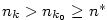
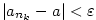
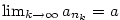
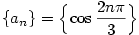

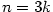
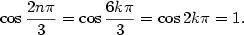
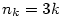
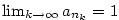
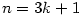
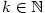
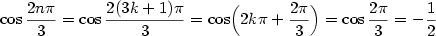
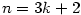
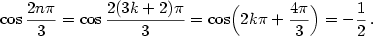
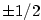
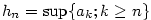
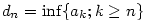
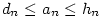
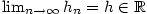
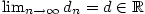
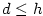
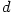
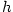
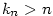
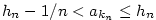
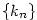
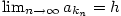
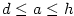
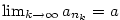
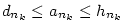
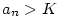
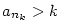
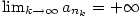
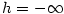
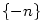
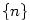
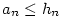
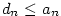
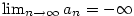
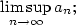
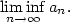
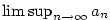

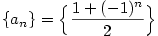
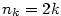
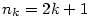
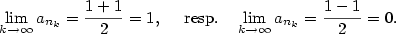
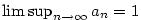
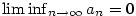
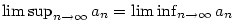
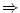
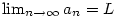
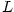
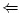
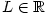
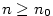
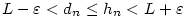
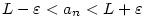
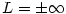
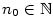
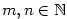
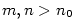
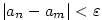
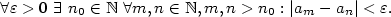
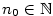

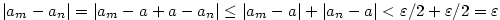 ,
,