1.1. Taylorova a Maclaurinova řada
V tomto učebním textu si ukážeme rozvoj funkce do
mocninné řady, tzv. Taylorovy řady.
Připomeňme Taylorovu větu z diferenciálního počtu,
kdy je funkce vyjádřena ve tvaru polynomu a
zbytku:
Nechť 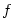 je funkce, která má derivace až do řádu 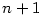
v uzavřeném intervalu 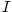 ,
jehož krajní body jsou čísla  a 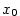 . Pak platí
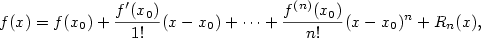
kde 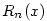 je Taylorův zbytek, pro který platí
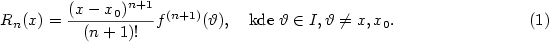
Je proto přirozené zavést následující definici:
Obecně nemusí platit, že součet Taylorovy řady funkce 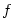 je roven
této funkci.
Následující dvě věty udávají podmínky, kdy tato rovnost platí.
Důkaz. Rovnost (1.5) platí na 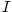 právě tehdy, když právě tehdy, když
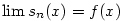 pro pro 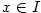 . Avšak . Avšak 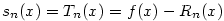 ,
takže ,
takže 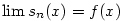 právě tehdy, když právě tehdy, když 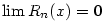 na na 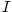 . .
|
Zobrazit / skrýt důkaz |
Poznámka 1.3.
Dá se ukázat, že lze-li funkci 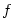 na nějakém intervalu na nějakém intervalu 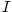 , jehož vnitřním bodem je , jehož vnitřním bodem je
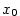 , rozvést do mocninné řady o středu , rozvést do mocninné řady o středu 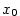 , pak je takový rozvoj
pouze jediný a je současně Taylorovým rozvojem funkce , pak je takový rozvoj
pouze jediný a je současně Taylorovým rozvojem funkce 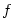 . .
|
Věta 1.4.
Nechť funkce 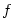 má
na otevřeném intervalu má
na otevřeném intervalu 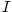 derivace
všech řádů a nechť posloupnost derivace
všech řádů a nechť posloupnost 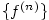 je
stejnoměrně ohraničená na je
stejnoměrně ohraničená na 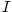 .
Pak Taylorova řada funkce .
Pak Taylorova řada funkce 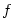 v libovolném
bodě v libovolném
bodě 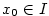 konverguje na
konverguje na 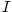 k k 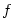 ,
tj. platí (1.5). ,
tj. platí (1.5).
|
Zobrazit / skrýt důkaz |
| Příklad 1.5. (Maclaurinovy řady elementárních funkcí)
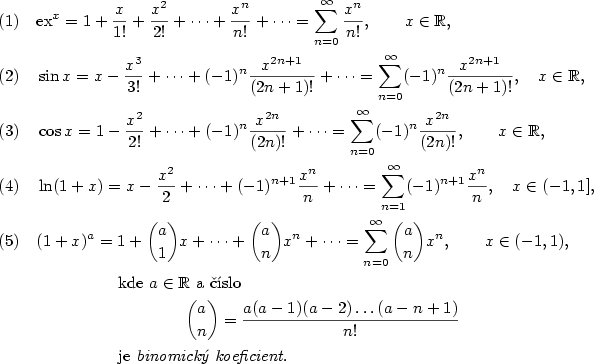
|
Řešení.
Ve většině případů byl tvar Maclaurinovy řady nalezen
v diferenciálním počtu, viz např. [9] Zbývá ověřit, že
součet Maclaurinovy řady dané funkce 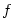 je právě tato funkce je právě tato funkce 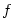 . .
(1) Je-li 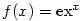 , pak , pak 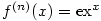 pro všechna pro všechna
 , takže je-li , takže je-li 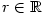 , , 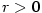 , je , je 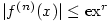 na na 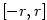 . Podle Věty 1.4 konverguje řada (1)
k . Podle Věty 1.4 konverguje řada (1)
k 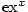 na na 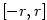 . Protože . Protože 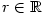 , , 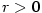 bylo libovolné,
platí tvrzení. bylo libovolné,
platí tvrzení.
(2) Protože 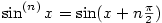 , pro , pro 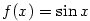 platí platí 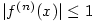 pro všechna pro všechna  a všechna a všechna
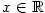 . Z Věty 1.4 pak plyne tvrzení. . Z Věty 1.4 pak plyne tvrzení.
(3) Důkaz tvrzení pro funkci 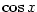 je analogické jako pro je analogické jako pro 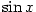 . .
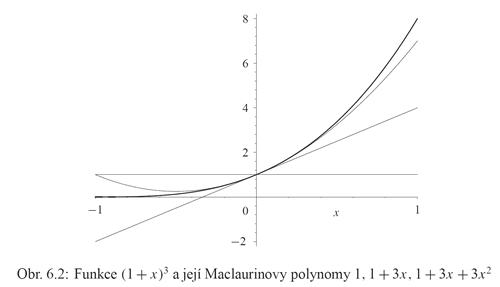
(4) VLOZIT Z PREDESLE KAPITOLY a je znázorněn na následujícím obrázku 6.1
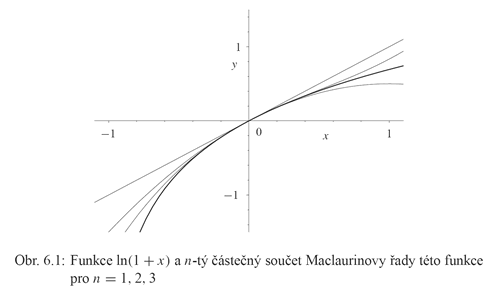
(5) Pro funkci 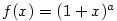 vyjádříme Taylorův zbytek
v Cauchyově tvaru [9]: vyjádříme Taylorův zbytek
v Cauchyově tvaru [9]:
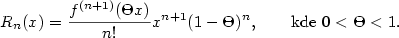
Pak platí
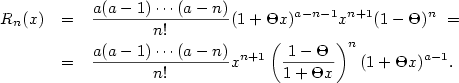
Je-li 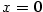 , je tvrzení věty zřejmé.
Je-li , je tvrzení věty zřejmé.
Je-li 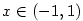 , , 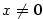 , pak řada , pak řada 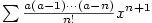 absolutně konverguje, jak se
snadno přesvědčíme podílovým kritériem.
Platí, že absolutně konverguje, jak se
snadno přesvědčíme podílovým kritériem.
Platí, že 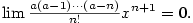 Dále platí
Dále platí
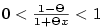 , tedy i , tedy i
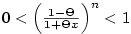 pro každé pro každé
 . .
Konečně je 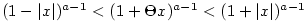 . Odtud . Odtud 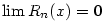 na intervalu na intervalu
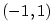 a tvrzení plyne z Věty 1.2. a tvrzení plyne z Věty 1.2.
|
Zobrazit / skrýt řešení |
| Příklad 1.7.
Rozviňte následující funkce do Maclaurinovy řady a určete jejich
obor konvergence:
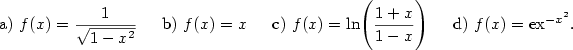
|
Zobrazit / skrýt řešení |
| Příklad 1.8.
Rozložte v Taylorovu řadu následující funkce:
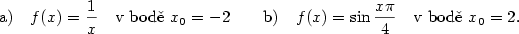
|
| Řešení.
a) Platí
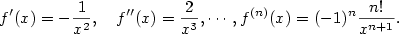
Dosazením do Taylorovy řady dostaneme
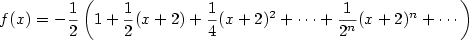
na intervalu 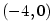 .
b) Postupujeme obdobně jako v předcházejícím případě: pro derivace
platí .
b) Postupujeme obdobně jako v předcházejícím případě: pro derivace
platí
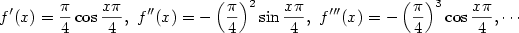
a po dosazení do Taylorovy řady
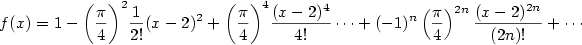
na intervalu 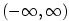 . .
|
Zobrazit / skrýt řešení |
Příklad 1.9.
Určete Maclaurinovu řadu funkce 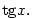
|
Zobrazit / skrýt řešení |
| Příklad 1.10.
Určete součet následujících mocninných řad:
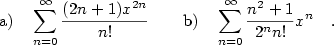
|
Zobrazit / skrýt řešení |
Historická poznámka. Nejjednodušším příkladem mocninné řady je geometrická řada
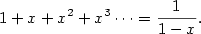
Historicky první mocninnou řadu, která není geometrická, objevili indičtí
matematici již v 15. století, a to řadu
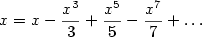
s jejím důležitým speciálním případem
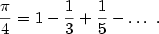
Bohužel, tento objev nebyl dlouho znám, a tím neovlivnil rozvoj
teorie mocninných řad. Teorie mocninných řad byla započata v době, kdy
N. Mercator publikoval (1668) řadu
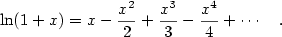
Racionální funkce, např. 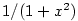 , lze rozvést pomocí geometrické řady;
rozhodující objev učinil I. Newton (1665), když objevil obecnou
binomickou řadu. Poté Newton odvodil řadu
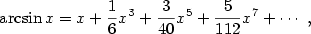
odkud pomocí inverze odvodil mocninnou řadu pro 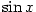 .
|














 je funkce, která má derivace až do řádu
je funkce, která má derivace až do řádu 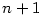 v uzavřeném intervalu
v uzavřeném intervalu 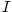 ,
jehož krajní body jsou čísla
,
jehož krajní body jsou čísla  a
a 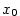 . Pak platí
. Pak platí
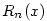 je Taylorův zbytek, pro který platí
je Taylorův zbytek, pro který platí
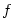 je roven
této funkci.
Následující dvě věty udávají podmínky, kdy tato rovnost platí.
je roven
této funkci.
Následující dvě věty udávají podmínky, kdy tato rovnost platí.
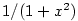 , lze rozvést pomocí geometrické řady;
rozhodující objev učinil I. Newton (1665), když objevil obecnou
binomickou řadu. Poté Newton odvodil řadu
, lze rozvést pomocí geometrické řady;
rozhodující objev učinil I. Newton (1665), když objevil obecnou
binomickou řadu. Poté Newton odvodil řadu
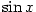 .
.
