rady_funkci.mws

Nekonecne rady s programem Maple

Nekonecne rady funci

Karel Srot, xsrot@math.muni.cz

>   

>    currentdir("c:/devel/maple/phd/export/"):

>   

Obor konvergence - metoda "krok za krokem"

zapisnik resi metodu vypoctu oboru konvergence rady funkci

>    restart:

>   

Nacteme proceduru csum , jejimz autorem je Robert B. Israel a je soucasti Maple Advisor Database 1.01 pro Maple 6. Slouzi pro test konvergence ciselnych rad.

>    read "csum5.txt":

>   

Priklad:

Urcete obor konvergence mocnine rady a sestrojte animaci ilustrujici konvergenci teto rady.

>    a:=n->(x^n)/(n*(n+1));

a := n -> x^n/n/(n+1)

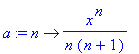
Obor konvergence nalezneme pomoci podiloveho kriteria a resime, pro ktera x je splnena podminka konvergence.

>    assume(x::real, n::posint):

>    abs(a(n+1)/a(n));

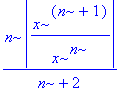
1/(n+2)*n*abs(x^(n+1)/(x^n))

>    simplify(%);

n*abs(x)/(n+2)

>    L:=limit(%, n=infinity);

L := abs(x)

>    solve(L<1);

RealRange(Open(-1),Open(1))

>    infolevel[csum]:=2:

pomoci procedury csum  resime konvergenci v krajnich bodech intervalu

>    csum(subs(x=1, a(n)), n); 

csum:   Checking sum of   1/n/(n+1)   over   n

csum/limitzero:   Checking limit of terms

csum/glimit:   "glimit is not available, will use limit"

csum/limitzero:   OK, limit is 0

csum/ratiotest:   Trying ratio test

csum/ratiotest:   Ratio test inconclusive with ratio limit   1

csum/loglogtest:   Trying loglog test

csum/loglogtest:   Loglog test succeeds

csum:   Series   1/n/(n+1)   converges absolutely

true

>    csum(subs(x=1, a(n)), n); 

csum:   Checking sum of   1/n/(n+1)   over   n

csum/limitzero:   Checking limit of terms

csum/limitzero:   OK, limit is 0

csum/ratiotest:   Trying ratio test

csum/ratiotest:   Ratio test inconclusive with ratio limit   1

csum/loglogtest:   Trying loglog test

csum/loglogtest:   Loglog test succeeds

csum:   Series   1/n/(n+1)   converges absolutely

true

>   

muzeme se take pokusit nalezt soucet rady

>    s:=sum((x^n)/(n*(n+1)), n=1..infinity);

s := 1+(1-x)/x*ln(1-x)

animaci znazornujici konvergenci rady

>    g1:=plot(s, x=-1..1, thickness=2, color=green):

>    g:=seq(plots[display](plot(sum((x^n)/(n*(n+1)), n=1..k), x=-1.5..1.5, y=-2..2, numpoints=200), g1), k=1..30):

>    plots[display](g, insequence=true);

[Maple Plot]

>   

Priklad:

Urcete obor konvergence mocnine rady.

>    a:=n->exp(-n^2*x);

a := n -> exp(-n^2*x)

>    assume(x::real, n::posint):

>    abs(a(n)^(1/n));

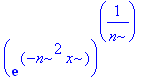
exp(-n^2*x)^(1/n)

>    simplify(%);

exp(-n*x)

>    limit(%, n=infinity);

limit(exp(-n*x),n = infinity)

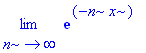
>    exp(limit(-n*x, n=infinity));

exp(-signum(x)*infinity)

>    solve(%<1, x);

RealRange(Open(0),infinity)

>    csum(subs(x=0, a(n)), n); 

csum:   Checking sum of   exp(0)   over   n

csum/limitzero:   Checking limit of terms

csum/limitzero:   Diverges, limit of terms is    exp(0)

csum:   Series diverges

false

>   

>    s:=sum(exp(-n^2*x), n=0..infinity);

s := sum(exp(-n^2*x),n = 0 .. infinity)

>   

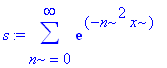
Priklad:

Urcete obor konvergence mocnine rady a vytvorte animaci ilustrujici konvergenci teto rady.

>    a:=n->ln(x)^n;

a := n -> ln(x)^n

>    assume(x::real, n::posint):

>    simplify(abs(a(n)^(1/n)), symbolic);

abs(ln(x))

>    solve(%<1, x);

RealRange(Open(1/exp(1)),Open(exp(1)))

>    simplify(subs(x=1/exp(1), a(n)));

(-1)^n

>    csum(%, n); 

csum:   Checking sum of   (-1)^n   over   n

csum:   Alternate terms   1   and   -1

csum/limitzero:   Checking limit of terms

csum/limitzero:   Diverges, limit of terms is    1

csum/alternate:   Series diverges

false

>    simplify(subs(x=exp(1), a(n)));

1

>    csum(%, n); 

csum:   Checking sum of   1   over   n

csum/limitzero:   Checking limit of terms

csum/limitzero:   Diverges, limit of terms is    1

csum:   Series diverges

false

>   

>    s:=sum(ln(x)^n, n=0..infinity);

s := -1/(ln(x)-1)

>    g1:=plot(s, x=exp(-1)..exp(1), thickness=2, color=green):

>    g:=seq(plots[display](plot(sum(ln(x)^n, n=0..k), x=(exp(-1)-0.05)..2.8, y=-1..50, numpoints=200), g1), k=1..40):

>    plots[display](g, insequence=true);

[Maple Plot]

>   

Priklad:

Urcete obor konvergence mocnine rady

>    a:=n->x^n*tan(x/2^n);

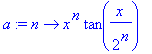
a := n -> x^n*tan(x/(2^n))

>    assume(x::real, n::posint):

>    simplify(abs(a(n+1)/a(n)));

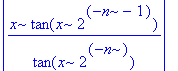
abs(x*tan(x*2^(-n-1))/tan(x*2^(-n)))

>    limit(%, n=infinity);

limit(abs(x*tan(x*2^(-n-1))/tan(x*2^(-n))),n = infinity)

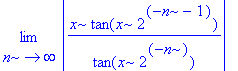
>    solve(%<1, x); 

Warning, solutions may have been lost

>    subs(x=-2, a(n));

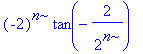
(-2)^n*tan(-2/(2^n))

>    csum(%, n); 

csum:   Checking sum of   -(-2)^n*tan(2/(2^n))   over   n

csum:   Alternate terms   -4^k*tan(2*4^(-k))   and   2*4^k*tan(4^(-k))

csum/limitzero:   Checking limit of terms

csum/limitzero:   Diverges, limit of terms is    -2

csum/alternate:   Series diverges

false

>    subs(x=2, a(n));

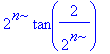
2^n*tan(2/(2^n))

>    simplify(%);

2^n*tan(2^(1-n))

>    csum(%, n); 

csum:   Checking sum of   2^n*tan(2^(1-n))   over   n

csum/limitzero:   Checking limit of terms

csum/limitzero:   Diverges, limit of terms is    2

csum:   Series diverges

false

>   

Priklad:

Urcete obor konvergence mocnine rady

>    a:=(n,x)->n/((n+1)*(3*x^2+4*x+2)^n);

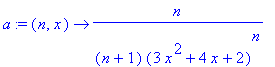
a := (n, x) -> n/(n+1)/((3*x^2+4*x+2)^n)

>    assume(x::real, n::posint):

>    simplify(abs(a(n+1,x)/a(n,x)));

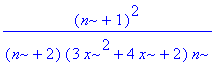
(n+1)^2/(n+2)/(3*x^2+4*x+2)/n

>    limit(%, n=infinity);

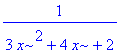
1/(3*x^2+4*x+2)

>    solve(%<1, x);

RealRange(-infinity,Open(-1)), RealRange(Open(-1/3),infinity)

>    csum(a(n,-1), n); 

csum:   Checking sum of   n/(n+1)   over   n

csum/limitzero:   Checking limit of terms

csum/limitzero:   Diverges, limit of terms is    1

csum:   Series diverges

false

>    csum(a(n,-1/3), n); 

csum:   Checking sum of   n/(n+1)   over   n

csum/limitzero:   Checking limit of terms

csum/limitzero:   Diverges, limit of terms is    1

csum:   Series diverges

false

>   

>    sum(n/((n+1)*(3*x^2+4*x+2)^n), n=0..infinity);

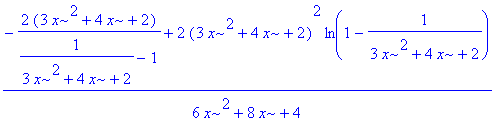
(-2*(3*x^2+4*x+2)/(1/(3*x^2+4*x+2)-1)+2*(3*x^2+4*x+2)^2*ln(1-1/(3*x^2+4*x+2)))/(6*x^2+8*x+4)

>   

Priklad:

Pomoci Weierstrassova kriteria rozhodnete o stejnomerne konvergenci zadane rady.

>    restart:

>    Sum(sin(n*x)*cos(n*x)/n^2,n=1..infinity);

Sum(sin(n*x)*cos(n*x)/n^2,n = 1 .. infinity)

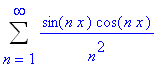
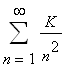Rada sum(K/(n^2),n = 1 .. infinity)    je pro pevne zvolene K  absolutne konvergentní. Pokud dokazeme, ze je funkce sin(n*x)  ohranicena (shora i zdola), bude i nami zkoumana rada stejnomerne konvergentni.

>    expr:=sin(n*x)*cos(n*x);

expr := sin(n*x)*cos(n*x)

Pokusime se najit obor hodnot tohoto vyrazu.

Funkce maximize  nevrati pozadovany vysledek.

>    maximize(expr,x=0..2*Pi,n=1..infinity); 

Error, (in maximize) sort: 2nd argument must be a function that always returns true or false

Dalsi moznosti je pouzit proceduru evalr , presto ani tento vysledek neni spravny.

>    evalr(subs(x=INTERVAL(0..2*Pi),expr));

INTERVAL(-1 .. 1)

presvedcime se o tom upravou vyrazu

>    convert(expr,sin);

1/2*sin(2*n*x)

>    evalr(subs(x=INTERVAL(0..2*Pi),%));

INTERVAL(-1/2 .. 1/2)

>   

>   

Obor konvergence - procedura TestSeriesConvergence

>    restart:

>    read "posl_a_rady_fci_proc.mpl":

>    infolevel[TestSeriesConvergence]:=2:

>   

Tato sekce ilustruje na nekolika prikladech pouziti procedury TestSeriesConvergence  pro nalezeni oboru konvergence nekonecne rady funci.

Priklad:

Pomoci procedury TestSeriesConvergence  se pokuste nalezt obory konvergence nasledujicich funkcnich rad.

>    (x^n)/(n*(n+1));

x^n/n/(n+1)

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   abs(x)

TestSeriesConvergence:   Range solved:   RealRange(Open(-1),Open(1))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Converges at point   x   =   -1

TestSeriesConvergence:   Converges at point   x   =   1

RealRange(-1,1)

>   

>    exp(-n^2*x);

exp(-n^2*x)

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   exp(-signum(x)*infinity)

TestSeriesConvergence:   Range solved:   RealRange(Open(0),infinity)

TestSeriesConvergence:   Checking isolated points

RealRange(Open(0),infinity)

>   

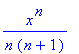
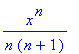
>    (x^n)/(n*(n+1));

x^n/n/(n+1)

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   abs(x)

TestSeriesConvergence:   Range solved:   RealRange(Open(-1),Open(1))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Converges at point   x   =   -1

TestSeriesConvergence:   Converges at point   x   =   1

RealRange(-1,1)

>   

>    ln(x)^n;

ln(x)^n

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   1

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   abs(ln(x))

TestSeriesConvergence:   Range solved:   RealRange(Open(1/exp(1)),Open(exp(1)))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Diverges at point   x   =   exp(1)

TestSeriesConvergence:   Test failed at point   x   =   1/exp(1)

RealRange(Open(1/exp(1)),Open(exp(1)))

>   

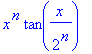
>    x^n*tan(x/2^n);

x^n*tan(x/(2^n))

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Ratio test failed: cannot find the limit

TestSeriesConvergence:   Trying root test

TestSeriesConvergence:   Root test failed: cannot find the limit

FAIL

>   

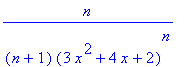
>    n/((n+1)*(3*x^2+4*x+2)^n);

n/(n+1)/((3*x^2+4*x+2)^n)

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   1/(3*x^2+4*x+2)

TestSeriesConvergence:   Range solved:   RealRange(-infinity,Open(-1)), RealRange(Open(-1/3),infinity)

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Diverges at point   x   =   -1

TestSeriesConvergence:   Diverges at point   x   =   -1/3

RealRange(-infinity,Open(-1)), RealRange(Open(-1/3),infinity)

>   

>    (x-1)*(x+1)*n;

(x-1)*(x+1)*n

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   -1, 1

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   1

TestSeriesConvergence:   Cannot resolve

FAIL

>   

>    (n!)^2/(2*n)!*x^n;

n!^2/(2*n)!*x^n

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   1/4*abs(x)

TestSeriesConvergence:   Range solved:   RealRange(Open(-4),Open(4))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Diverges at point   x   =   -4

TestSeriesConvergence:   Diverges at point   x   =   4

RealRange(Open(-4),Open(4))

>   

>    (-1)^(n-1)*x^(2*n)/sqrt(n)/(2*n-1);

(-1)^(n-1)*x^(2*n)/n^(1/2)/(2*n-1)

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   x^2

TestSeriesConvergence:   Range solved:   RealRange(Open(-1),Open(1))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Converges at point   x   =   1

TestSeriesConvergence:   Converges at point   x   =   -1

RealRange(-1,1)

>   

>    (-1)^n*(x+2)^n/(n+sqrt(n));

(-1)^n*(x+2)^n/(n+n^(1/2))

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   -2

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   abs(x+2)

TestSeriesConvergence:   Range solved:   RealRange(Open(-3),Open(-1))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Diverges at point   x   =   -3

TestSeriesConvergence:   Converges at point   x   =   -1

RealRange(Open(-3),-1)

>   

>    x^n/n;

x^n/n

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   abs(x)

TestSeriesConvergence:   Range solved:   RealRange(Open(-1),Open(1))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Converges at point   x   =   -1

TestSeriesConvergence:   Diverges at point   x   =   1

RealRange(-1,Open(1))

>   

>    (-1)^n*(x+2)^n/(n+sqrt(n));

(-1)^n*(x+2)^n/(n+n^(1/2))

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   -2

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   abs(x+2)

TestSeriesConvergence:   Range solved:   RealRange(Open(-3),Open(-1))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Diverges at point   x   =   -3

TestSeriesConvergence:   Converges at point   x   =   -1

RealRange(Open(-3),-1)

>   

>    x/n;

x/n

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   1

TestSeriesConvergence:   Cannot resolve

FAIL

>   

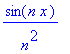
>    sin(n*x)/n^2;

sin(n*x)/n^2

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   0

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Ratio test failed: cannot find the limit

TestSeriesConvergence:   Trying root test

TestSeriesConvergence:   Root test failed: cannot find the limit

FAIL

>   

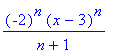
>    (-2)^n*(x-3)^n/(n+1);

(-2)^n*(x-3)^n/(n+1)

>    TestSeriesConvergence(%,n,x); 

TestSeriesConvergence:   Series identical zero when    x   =   3

TestSeriesConvergence:   Trying ration test

TestSeriesConvergence:   Limit:   2*abs(x-3)

TestSeriesConvergence:   Range solved:   RealRange(Open(5/2),Open(7/2))

TestSeriesConvergence:   Checking isolated points

TestSeriesConvergence:   Diverges at point   x   =   5/2

TestSeriesConvergence:   Converges at point   x   =   7/2

RealRange(Open(5/2),7/2)

>   

>   

Obor konvergence  - animace

>    restart;

>    read "posl_a_rady_fci_proc.mpl":

>   

Pri vytvareni animaci vyuzijeme proceduru plotVerticalStrip, ktera slouzi pro "ohraniceni" oboru konvergence. Jako prvni z parametru proceduru prebira obor konvergence a jako druhy parametr vertikalni rozsah grafu, napr.

>    plotVerticalStrip(RealRange(-1,Open(1)),-5..5);

[Maple Plot]

>   

>   

Priklad:

Prostrednictvim animace ilustrujte chovani (konvergenci) zadane rady uvnitr a vne oboru konvergence teto rady.

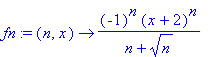
>    fn:=(n,x)->(-1)^n*(x+2)^n/(n+sqrt(n));

fn := (n, x) -> (-1)^n*(x+2)^n/(n+sqrt(n))

nalezneme obor konvergence

>    TestSeriesConvergence(fn(n,x),n,x);

RealRange(Open(-3),-1)

sestrojime animaci jednotlivych clenu rady - nutna podminka konvergence vyzaduje, aby se cleny rady limitne blizily k funkci y=0.

>    strip:=plotVerticalStrip(RealRange(Open(-3),-1),-2..2):

>    graf:=n->plots[display](strip,plot(fn(n,x),x=-4..0,y=-2..2,thickness=2)):

>    plots[display](seq(graf(i),i=1..15), insequence=true,scaling=constrained);

[Maple Plot]

>   

sestrojime animaci castecnych souctu nekonecne rady

>    sn:=(n,x)->sum(fn(k,x),k=1..n);

sn := (n, x) -> sum(fn(k,x),k = 1 .. n)

>    strip:=plotVerticalStrip(RealRange(Open(-3),-1),-1.5..4):

>    graf:=n->plots[display](strip,plot(sn(n,x),x=-4..0,y=-1.5..4,thickness=2)):

>    plots[display](seq(graf(i),i=1..15), insequence=true,scaling=constrained);

[Maple Plot]

>   

>