FourierTrigSeries package
Karel Srot, xsrot@math.muni.cz, www.math.muni.cz/~kriz/xsrot/fourierseries
Faculty of Science, Masaryk University, Czech Republic
This package concept differs from other Fourier series packages. It provides new data structure for the representation of trigonometric series and few procedures to manipulate trigonometric series and to compute Fourier series. Some procedures and data structure are (for better understanding) similar (but not exactly the same) to OrthogonalSeries package so in many cases you can use the OrthogonalSeries package help files.
| > |
| > | restart: |
| > | with(FourierTrigSeries); |
![]()
![]()
![]()
| > |
Create()
Usage of the procedure Create is similar to OrthogonalSeries[Create] but there are few differences.
| > | s:=Create({[1,2,3], n}, SinTrigP(n,x)); |
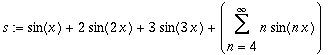
| > | type(s, FOURIERSERIES); |
![]()
There are four types of orthogonal systems: SinTrigP, CosTrigP, CosSinTrigP and ExpTrigP2. ExpTrigP2 means that the series is defined as a sum which goes from the zero to the plus infinity (and not from the minus infinity to the plus infinity).
| > | Create({[1,2,3], n}, CosTrigP(n,x)); |
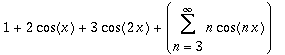
Creating series with different period.
| > | Create({[1,2,3], n}, CosTrigP(n,x), Pi); |
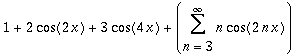
When creating the series with both sine and cosine terms, the coefficients are specified by a list of pairs. Also it is necessary to use the option "general" to set the general coefficient of the series.
| > | s:=Create({[1,[1,-1],[1/2,-1/2]], 'general'=[n,-n]}, CosSinTrigP(n,x)); |
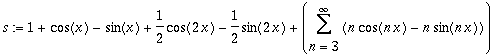
Some other possibilities to specify the coefficients (see OrthogonalSeries[Create]):
| > | Create({[1,[1,-1],[1/2,-1/2]]}, CosSinTrigP(n,x)); |
![]()
| > | Create({[0=1,1=[1,-1],3=[1/2,-1/2]], 'general'=n, n=5..10}, CosSinTrigP(n,x)); |
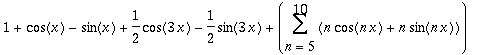
| > | Create({[0=1,1=[1,-1],3=[1/2,-1/2]], 'general'=n, n=5..10}, ExpTrigP2(n,x)); |
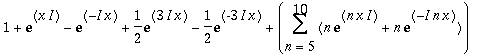
The data structure of the type FOURIERSERIES:
| > | lprint(s); |
FourierTrigSeries:-FOURIERSERIES(S)
| > | print(op(1,s)); |
![]()
![]()
![]()
![]()
ConvertToSum()
Converting series structure to the regular sum
| > | ConvertToSum(s); |
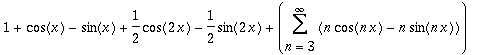
| > | lprint(%); |
1+cos(x)-sin(x)+1/2*cos(2*x)-1/2*sin(2*x)+Sum(n*cos(n*x)-n*sin(n*x),n = 3 .. infinity)
Derivate()
Derivate the series
| > | s2:=Derivate(s, 'x'); |
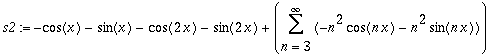
| > | s3:=Create({[t], t*n}, CosTrigP(n,x)); |
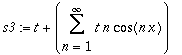
| > | Derivate(s3, 'x'); |
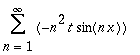
| > | Derivate(s3, 't'); |
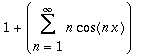
Evaluate(), GetPartialSum()
Evaluation
| > | Evaluate(s, x=Pi/4); |
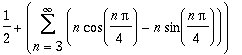
| > | Evaluate(s, trunc=5); |
![]()
The same can be obtained by
| > | GetPartialSum(s, 5); |
![]()
| > | Evaluate(s, x=Pi/4, trunc=5); |
![]()
| > | Evaluate(s, x=A, trunc=5); |
![]()
ChangeBasis()
Conversion between orthogonal systems.
| > | s2; |
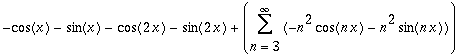
| > | ChangeBasis(s2, `ExpTrigP2`(n,x)); |
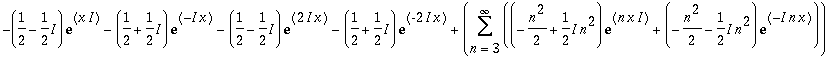
| > | ChangeBasis(%, `SinTrigP`(n,x)); |
![]()
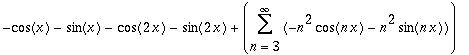
Add(), ScalarMultiply()
Adding two series and multiplying the series by a scalar.
| > | s; |
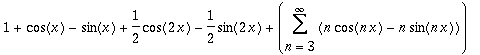
| > | s2; |
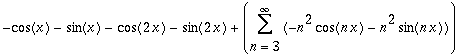
| > | Add(s,s2); |
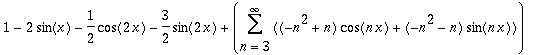
| > | Add(s,s2, 1, 3); |
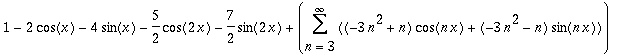
| > | s3:=ScalarMultiply(s2, (1-alpha)); |
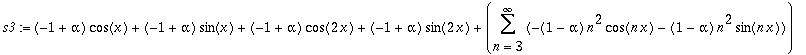
Coefficient(), Degree(), Truncate(), Copy()
Getting the coefficients and the degree of the partial sum, copying the series.
| > | s; |
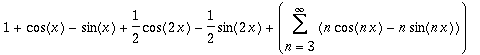
| > | Coefficients(s,5); |
![]()
| > | Degree(s3); |
![]()
| > | Truncate(s3,7); |
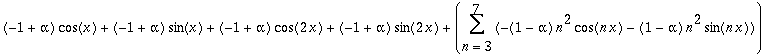
| > | Degree(%); |
![]()
Copying the series
| > | s4:=Copy(s3); |
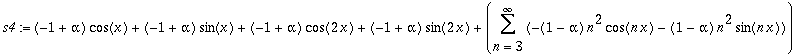
SimplifyCoefficients()
Simplify the coefficients
| > | s1:=Create({-1/(n-1)}, SinTrigP(n,x)); |
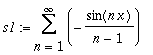
| > | s2:=Create({n/(n-1)}, SinTrigP(n,x)); |
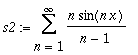
| > | Add(s1,s2); |
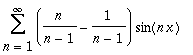
| > | SimplifyCoefficients(%, simplify); |
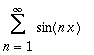
GetFourierSeries()
Computing the Fourier series of the given function.
| > | GetFourierSeries(cos(x)^4,x=-Pi..Pi); |
![]()
| > | GetFourierSeries(x+signum(x),x=-Pi..Pi); |
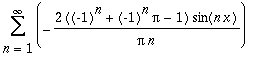
Getting the partial sum.
| > | t:=Truncate(%, 4); |

| > | ConvertToSum(t); |
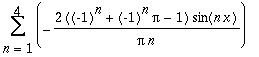
Change the orthogonal system.
| > | ChangeBasis(t, `ExpTrigP2`(n,x)); |
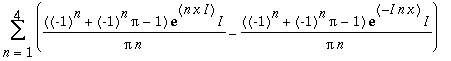
| > | GetFourierSeries(x^2,x=-Pi..Pi, exp); |
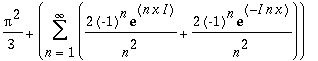
Getting the Fourier series of the odd/even periodic extension.
| > | GetFourierSeries(x^2,x=0..Pi, even); |
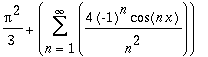
| > | GetFourierSeries(x^2,x=0..Pi, even, exp); |
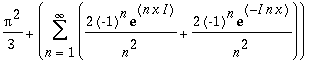
| > | GetFourierSeries(x^3,x=-Pi..Pi); |
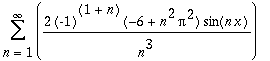
| > | GetFourierSeries(x^3,x=-Pi..0, odd); |
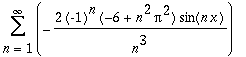
| > |
ExploreFourierSeriesCoefficients()
Procedure computes values of Fourier series coefficients
| > | ExploreFourierSeriesCoefficients(signum(sin(2*x)), x=-Pi..Pi); |
![1/2*a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images4/examples55.gif)
![]()
![b[n] = 2*((-1)^n+1-2*cos(1/2*Pi*n))/Pi/n](images4/examples57.gif)
Look at coefficients in more detail
| > | ExploreFourierSeriesCoefficients(signum(sin(2*x)), x=-Pi..Pi,2); |
![1/2*a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images4/examples58.gif)
![]()
![b[n] = PIECEWISE([-2*(-1+(-1)^k)/Pi/k, n = 2*k],[0, n = 2*k+1])](images4/examples60.gif)
| > | ExploreFourierSeriesCoefficients(signum(sin(2*x)), x=-Pi..Pi,4); |
![1/2*a[0]+Sum(a[n]*cos(n*x)+b[n]*sin(n*x),n = 1 .. infinity)](images4/examples61.gif)
![]()
![b[n] = PIECEWISE([0, n = 4*k],[0, n = 4*k+1],[4/Pi/(2*k+1), n = 4*k+2],[0, n = 4*k+3])](images4/examples63.gif)
| > | ExploreFourierSeriesCoefficients(signum(sin(2*x)), x=-Pi..Pi, 4, exp); |
![c[0]+Sum(c[n]*exp(n*x*I)+c[-n]*exp(-I*n*x),n = 1 .. infinity)](images4/examples64.gif)
![]()
![c[n] = PIECEWISE([0, n = 4*k],[0, n = 4*k+1],[-2*I/Pi/(2*k+1), n = 4*k+2],[0, n = 4*k+3])](images4/examples66.gif)
![c[-n] = PIECEWISE([0, n = 4*k],[0, n = 4*k+1],[2*I/Pi/(2*k+1), n = 4*k+2],[0, n = 4*k+3])](images4/examples67.gif)
DrawPartialSum()
| > | S:=GetFourierSeries(x,x=-1..1): |
| > | DrawPartialSum(S,3); |
![[Maple Plot]](images4/examples68.gif)
| > | DrawPartialSum(S,3,-2..2,scaling=constrained,color=blue,thickness=3); |
![[Maple Plot]](images4/examples69.gif)
| > |
DrawPeriodicExtension()
| > | DrawPeriodicExtension(x,x=-1..1,-2..2); |
![[Maple Plot]](images4/examples70.gif)
| > | DrawPeriodicExtension(x,x=0..1,-3..3,even,thickness=3,color=blue,scaling=constrained); |
![[Maple Plot]](images4/examples71.gif)
| > | DrawPeriodicExtension(x^2,x=-1..0,-2..2,odd,drawlimits,scaling=constrained); |
![[Maple Plot]](images4/examples72.gif)
| > |
Solving the differential equation using the Fourier series.
| > | Diff(y(x),x$2)+2*y(x)=Sum(sin(n*x)/n^4,n=1..infinity); |
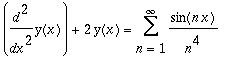
| > | S1:=Create({[0],'general'=[0,1/n^4]}, CosSinTrigP(n,x)); |
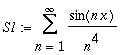
Create the general series
| > | S2:=Create({[a0], 'general'=[aN,bN]}, CosSinTrigP(n,x)); |
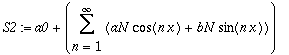
Derivate the series two times
| > | tmp1:=Derivate(Derivate(S2, 'x'), 'x'); |
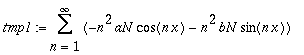
Add the multiple of the series
| > | tmp2:=Add(tmp1,S2, 1, 2); |
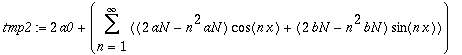
Our equation now has the form
| > | tmp2=S1; |
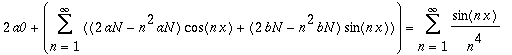
Subtract the series
| > | S:=Add(lhs(%), rhs(%), 1, -1); |
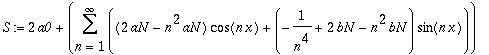
| > | type(S, FOURIERSERIES); |
![]()
Series S should have all coefficients equal to zero. Hence a0 = 0.
Get the general coefficient.
| > | Coefficients(S); |
![]()
| > | {%[1]=0, %[2]=0}; |
![]()
| > | solve(%, {aN, bN}); |
![]()
Create the solution.
| > | Y:=Create({subs(%, bN)}, SinTrigP(n,x)); |
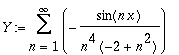
Check the solution
| > | Add(Derivate(Derivate(Y, 'x'), 'x'), Y, 1, 2); |
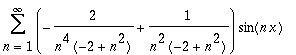
| > | SimplifyCoefficients(%, simplify); |
| > |
| > |
| > |