|
Zopakujme nejdříve ještě jednou znění Lemmatu 1.1.
Lemma 1.1 (Cauchyovo-Bolzanovo kritérium konvergence).
Řada 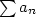 je konvergentní právě tehdy, když posloupnost jejích částečných součtů je Cauchyovská, tj. pro libovloné je konvergentní právě tehdy, když posloupnost jejích částečných součtů je Cauchyovská, tj. pro libovloné 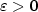 existuje existuje 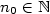 takové, že pro takové, že pro 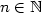 , ,  a libovolné a libovolné 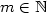 platí platí
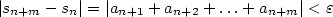
Rozeberme si případ Cauchyovské posloupnosti podrobněji pomocí následujícího obrázku.
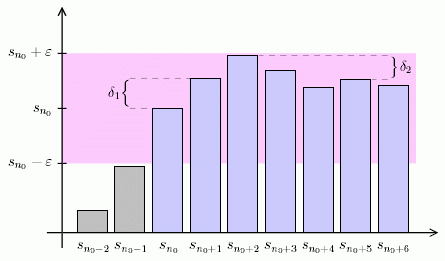
Pro libovolné (tedy i libovolně malé)  najdeme přirozené číslo najdeme přirozené číslo 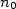 takové, že jakékoliv dva částečné součty s indexem alespoň takové, že jakékoliv dva částečné součty s indexem alespoň 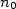 (vyznačeny modrou barvou) mají rozdíl v absolutní hodnotě menší než námi zvolené (vyznačeny modrou barvou) mají rozdíl v absolutní hodnotě menší než námi zvolené  . V obrázku jsou dva takové rozdíly označeny . V obrázku jsou dva takové rozdíly označeny 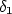 a a 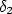 . .
Ve speciálním případě to znamená, že zvolíme-li pevně jeden částečný součet (v obrázku součet 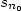 ), budou všechny následující částečné součty ležet v ), budou všechny následující částečné součty ležet v  -ovém pásu kolem tohoto částečného součtu (vyplněn růžovou barvou). -ovém pásu kolem tohoto částečného součtu (vyplněn růžovou barvou).
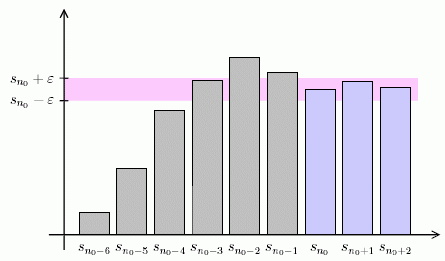
Jak již bylo zmíněno dříve, tento pás může být libovolně malý (druhý obrázek znázorňuje situaci při jinak zvoleném  ). Z úplnosti ). Z úplnosti 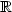 plyne, že limitou této posloupnosti částečných součtů (a tedy i součtem řady), je reálné číslo. plyne, že limitou této posloupnosti částečných součtů (a tedy i součtem řady), je reálné číslo.
| 




