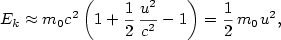Kapitola 7Přibližné vyjádření funkce
V této kapitole ukážeme, jak lze přibližně určovat funkční hodnoty
funkce  v okolí daného bodu, tj. lokálně .
Zadanou funkci nahradíme (aproximujeme) nějakou jednodušší funkcí. V našem případě
budeme používat polynomy. Nejjednodušší aproximace je pomocí lineárního
polynomu, kdy přírůstek funkce zaměňujeme lineární funkcí — tzv. diferenciálem.
Aproximujeme-li funkci obecně polynomem stupně v okolí daného bodu, tj. lokálně .
Zadanou funkci nahradíme (aproximujeme) nějakou jednodušší funkcí. V našem případě
budeme používat polynomy. Nejjednodušší aproximace je pomocí lineárního
polynomu, kdy přírůstek funkce zaměňujeme lineární funkcí — tzv. diferenciálem.
Aproximujeme-li funkci obecně polynomem stupně 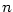 , mluvíme o Taylorově rozvoji. , mluvíme o Taylorově rozvoji.
Ilustrujme nejprve tento problém na příkladě: Chceme aproximovat
danou funkci 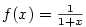 v okolí bodu v okolí bodu 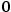 polynomem stupně polynomem stupně 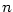 .
Použijeme vzorec pro součet nekonečné geometrické řady, podle kterého .
Použijeme vzorec pro součet nekonečné geometrické řady, podle kterého

Znamená to, že funkci 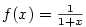 můžeme v okolí bodu můžeme v okolí bodu 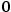 s určitou chybou nahradit funkcí s určitou chybou nahradit funkcí
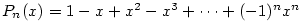 .
Říkáme, že funkci .
Říkáme, že funkci  „lokálně
aproximujeme” (tj. nahrazujeme) polynomem stupně „lokálně
aproximujeme” (tj. nahrazujeme) polynomem stupně 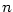 . .
7.1. Diferenciál
Definice 7.1.
Nechť funkce  je definovaná v okolí je definovaná v okolí 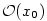 bodu bodu 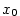 a platí a platí 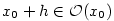 .
Pak číslo .
Pak číslo 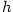 nazýváme přírůstkem nezávisle proměnné
a rozdíl nazýváme přírůstkem nezávisle proměnné
a rozdíl 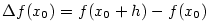 nazýváme přírůstkem funkce nazýváme přírůstkem funkce  v bodě
v bodě 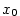 neboli přírůstkem závisle proměnné
— viz obr. 7.1. neboli přírůstkem závisle proměnné
— viz obr. 7.1.
|
Naším cílem bude vyšetřit vyjádření přírůstku 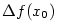 v závislosti na čísle v závislosti na čísle 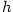 .
Nejjednodušší případ je obsahem následující definice.
Následující věta udává vztah mezi diferencovatelností funkce a její derivací.
Uvědomte si, že z předchozí věty vyplývá, že konstanta .
Nejjednodušší případ je obsahem následující definice.
Následující věta udává vztah mezi diferencovatelností funkce a její derivací.
Uvědomte si, že z předchozí věty vyplývá, že konstanta 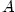 a funkce a funkce 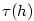 z definice 7.2 jsou určeny jednoznačně.
Nechť existuje diferenciál
z definice 7.2 jsou určeny jednoznačně.
Nechť existuje diferenciál 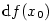 funkce funkce  v bodě v bodě 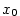 .
Snadno se ověří, že platí .
Snadno se ověří, že platí
Je-li 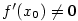 , platí rovněž , platí rovněž

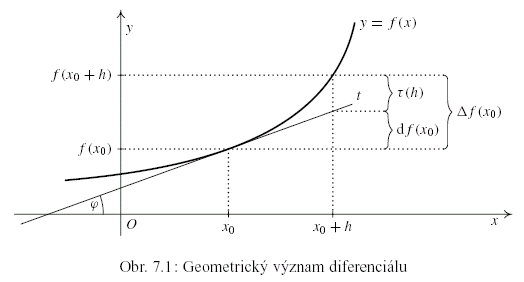
Geometrický význam diferenciálu.
Víme již, že vlastnost „mít diferenciál” je rovnocenná vlastnosti „mít derivaci”.
Sestrojme tečnu 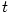 ke grafu funkce ke grafu funkce  v bodě v bodě 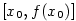 — viz obr. 7.1.
Pak platí — viz obr. 7.1.
Pak platí 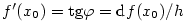 . Přírůstek . Přírůstek 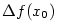 je součtem dvou hodnot:
diferenciálu je součtem dvou hodnot:
diferenciálu 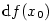 a a 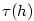 . Ze vztahů (7.1) a (7.2) je vidět, že pro malá . Ze vztahů (7.1) a (7.2) je vidět, že pro malá 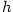 je (je-li
je (je-li 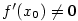 ) ) 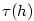 mnohem menší než diferenciál.
Nejběžnější aplikace diferenciálu spočívá v tom, že (pro malá mnohem menší než diferenciál.
Nejběžnější aplikace diferenciálu spočívá v tom, že (pro malá  )
klademe )
klademe
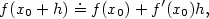
tj. skutečný přírůstek funkce 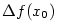 nahradíme s jistou chybou diferenciálem nahradíme s jistou chybou diferenciálem
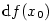 (geometricky graf funkce nahradíme její tečnou). Někdy se používá označení (geometricky graf funkce nahradíme její tečnou). Někdy se používá označení
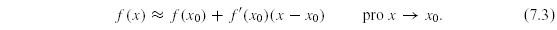
Příklad 7.4.
Vypočtěte přibližně 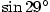 a a  . .
|
Řešení. Použijeme vzorec (7.3). Dostáváme
-
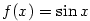 , , 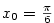 , , 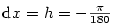 , ,
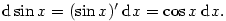
Aplikujeme diferenciál:
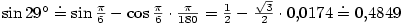 . Přesná hodnota je
po zaokrouhlení . Přesná hodnota je
po zaokrouhlení 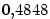 . .
-
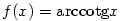 , diferenciál , diferenciál
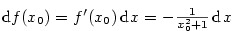 , , 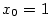 , , 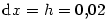 . S použitím diferenciálu dostaneme . S použitím diferenciálu dostaneme
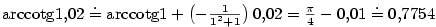 . Přesná hodnota je po zaokrouhlení . Přesná hodnota je po zaokrouhlení 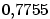 . .
|
Zobrazit / skrýt řešení |
Nechť  má derivaci na množině má derivaci na množině 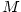 . Pak pro každé . Pak pro každé 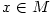 je definován
diferenciál je definován
diferenciál 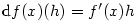 , tj. diferenciální funkce.
Je to funkce dvou proměnných: nezávislé proměnné , tj. diferenciální funkce.
Je to funkce dvou proměnných: nezávislé proměnné 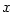 a přírůstku nezávisle proměnné a přírůstku nezávisle proměnné 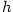 . .
Pro lineární funkci 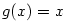 platí platí 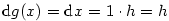 . Tato rovnost vysvětluje, proč
pro označení přírůstku nezávisle proměnné používáme rovněž symbol . Tato rovnost vysvětluje, proč
pro označení přírůstku nezávisle proměnné používáme rovněž symbol 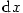 . Pro diferenciál funkce . Pro diferenciál funkce  pak máme
pak máme 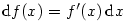 , odkud plyne , odkud plyne 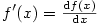 , což zdůvodňuje označení
pro derivaci funkce , což zdůvodňuje označení
pro derivaci funkce  symbolem symbolem 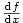 . Při tomto označení (pocházejícím od Leibnize,
označení čárkou zavedl Lagrange) mají některé vzorce pro derivování názorný tvar. Například: . Při tomto označení (pocházejícím od Leibnize,
označení čárkou zavedl Lagrange) mají některé vzorce pro derivování názorný tvar. Například:
Řešení.
Položme 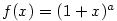 , , 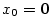 . Pak . Pak 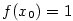 , , 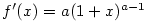 a a 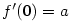 . Odtud máme . Odtud máme
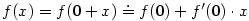 , tj. , tj. 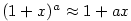 . .
Právě dokázaný vzorec aplikujme na konkrétní příklady. Platí:
-
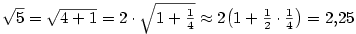 .
Můžeme ověřit, jak je naše aproximace přesná: Na kalkulačce najdeme (po zaokrouhlení) .
Můžeme ověřit, jak je naše aproximace přesná: Na kalkulačce najdeme (po zaokrouhlení)
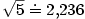 , a proto chyba, které jsme se aproximací dopustili, je , a proto chyba, které jsme se aproximací dopustili, je 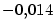 . .
-
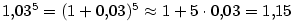 . .
-
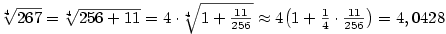 . .
|
Zobrazit / skrýt řešení |
Použití diferenciálu na řešení podobných úloh je v dnešní době archaismem. Přibližný vzorec ovšem
neztrácí smysl, pokud nemáme analytický předpis funkce 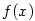 a hodnoty a hodnoty 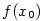 a a 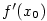 jsme
získali např. měřením. Zásadní význam má tento vztah rovněž
ve fyzice a pod. při odvozování nejrůznějších vzorců, kdy se vyšší
mocniny přírůstku (tj. u nás výraz jsme
získali např. měřením. Zásadní význam má tento vztah rovněž
ve fyzice a pod. při odvozování nejrůznějších vzorců, kdy se vyšší
mocniny přírůstku (tj. u nás výraz 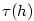 ) zanedbávají. Tyto členy vlastně zmizí při nějakém
limitním přechodu. Použití diferenciálu znamená linearizaci problému. ) zanedbávají. Tyto členy vlastně zmizí při nějakém
limitním přechodu. Použití diferenciálu znamená linearizaci problému.
Diferenciál se rovněž používá při odhadu tzv. absolutní chyby
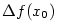 a relativní chyby a relativní chyby 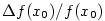 .
Klade se .
Klade se 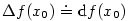 a a 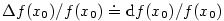 .
Toto použití ilustrují následující (velmi jednoduché) příklady. .
Toto použití ilustrují následující (velmi jednoduché) příklady.
Příklad 7.6.
Vypočtěte, o kolik se přibližně zvětší objem koule, jestliže za poloměr místo hodnoty
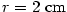 vezmeme hodnotu vezmeme hodnotu 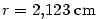 . Odhadněte relativní chybu výpočtu. . Odhadněte relativní chybu výpočtu.
|
Řešení.
Obecný vzorec pro výpočet objemu koule je 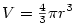 .
Platí .
Platí 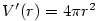 , a proto , a proto
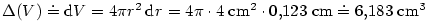 . .
Dále 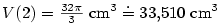 , tedy pro relativní chybu máme , tedy pro relativní chybu máme
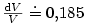 , tj. asi , tj. asi  .
Nebo .
Nebo 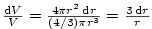 se stejným výsledkem. se stejným výsledkem.
Příklad je samozřejmě „školský”. Vzhledem k jednoduchosti vzorce je snadné získat
přesné hodnoty. Je 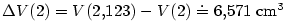 a a
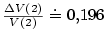 , tj. asi , tj. asi 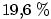 . .
|
Zobrazit / skrýt řešení |
Příklad 7.7.
Pomocí diferenciálu odhadněte, jaká je přibližná změna obsahu
kruhové výseče o úhlu 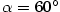 a poloměru a poloměru 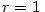 m m
- při zvětšení poloměru o
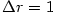 cm; cm;
- při zmenšení středového úhlu o
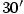 . .
|
Zobrazit / skrýt řešení |
7.2. Taylorův vzorec
Řešme problém zmíněný v úvodu této kapitoly:
Nechť má funkce  v bodě v bodě 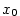 všechny derivace až do řádu všechny derivace až do řádu 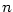 , které jsou vlastní.
Chceme funkci v okolí bodu , které jsou vlastní.
Chceme funkci v okolí bodu 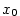 nahradit polynomem tvaru nahradit polynomem tvaru 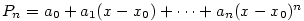 tak, aby polynom aproximoval funkci tak, aby polynom aproximoval funkci  co „nejpřesněji”.
Je jistě rozumné požadovat, aby co „nejpřesněji”.
Je jistě rozumné požadovat, aby

což je 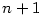 rovnic o neznámých rovnic o neznámých 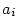 , kde , kde 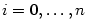 . Platí . Platí
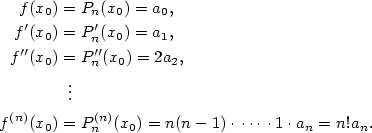
Odtud dostáváme hledaný polynom
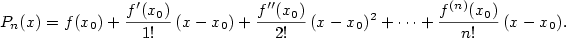
Tento polynom se nazývá Taylorův polynom stupně 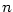 funkce funkce  se středem
se středem 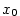 a značí se a značí se
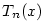 nebo podrobněji nebo podrobněji 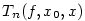 . Nahradíme-li funkci . Nahradíme-li funkci  v okolí
bodu v okolí
bodu 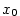 Taylorovým polynomem Taylorovým polynomem 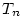 , dopustíme se chyby, kterou označujeme , dopustíme se chyby, kterou označujeme 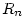 , tj. , tj.
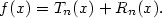
O velikosti této chyby mluví následující věta.
Důkaz viz dodatek, věta D54. Uvedené vyjádření zbytku je v tzv.
Lagrangeově tvaru.
Existují i jiné (složitější) tvary, které jsou pro odhady velikosti určitých typů zbytků vhodnější.
Maclaurinovy vzorce elementárních funkcí
V následujícím přehledu jsou uvedeny Maclaurinovy vzorce nejdůležitějších elementárních
funkcí. V níže uvedených vzorcích 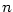 značí libovolné přirozené číslo a značí libovolné přirozené číslo a 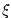 značí vhodné číslo
mezi značí vhodné číslo
mezi 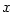 a nulou. a nulou.
- Pro každé
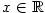 platí platí
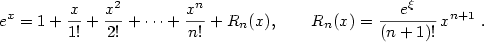
Zdůvodnění: 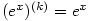 (důkaz provedeme indukcí), odkud (důkaz provedeme indukcí), odkud 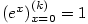 , , 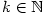 . .
- Pro každé
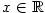 platí platí
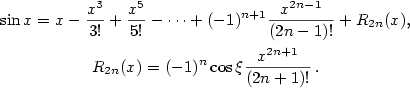
Zdůvodnění: 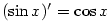 , , 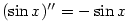 , ,
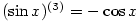 , , 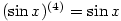 , odkud plyne pro , odkud plyne pro 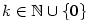
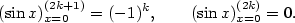
- Pro každé
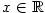 platí platí
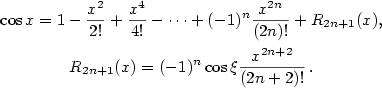
- Pro každé
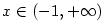 platí platí

Zdůvodnění: 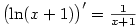 , , 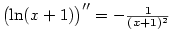 ,
obecně ,
obecně 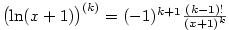 ,
tedy ,
tedy 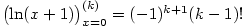 . .
-
Pro libovolná
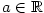 a a 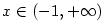 (v případě (v případě 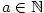 i pro i pro 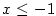 ) platí ) platí

kde pro 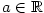 , , 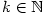 definujeme tzv. zobecněný binomický
koeficient definujeme tzv. zobecněný binomický
koeficient
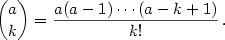
Maclaurinův vzorec mocninné funkce se někdy nazývá binomický vzorec.
Zdůvodnění: Pro derivace platí
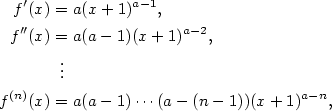
a proto
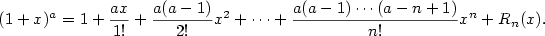
Poznámka 7.11. V případě 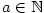 , , 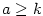 je definice zobecněného binomického koeficientu
ve shodě s definicí binomického čísla známou z elementární matematiky.
Speciálními případy binomického rozvoje jsou pro je definice zobecněného binomického koeficientu
ve shodě s definicí binomického čísla známou z elementární matematiky.
Speciálními případy binomického rozvoje jsou pro 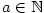 , , 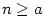 , binomická věta a pro , binomická věta a pro
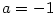 geometrická řada. Ověřte! geometrická řada. Ověřte!
|
Poznámka 7.13. Z Maclaurinových rozvojů exponenciály, sinu a kosinu je vidět (aspoň formálně,
exponenciální funkce nebyla pro komplexní hodnoty definována a hodnota zbytku
v komplexním čísle rovněž v této podobě nemá smysl),
proč platí tzv. Eulerův vztah 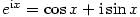 : :
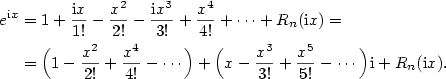
S přesným důkazem se seznámíte v teorii mocninných řad.
|
Příklad 7.14.
Napište Taylorův polynom 3. stupně v bodě 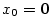 funkce funkce
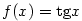 . .
|
Zobrazit / skrýt řešení |
7.3. Aplikace Taylorova vzorce
Pro další úvahy zaveďme následující symboly, které se často v matematické analýze používají.
Definice 7.15.
Nechť 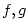 jsou funkce, jsou funkce, 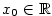 a nechť
existuje okolí a nechť
existuje okolí 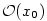 takové, že pro všechna takové, že pro všechna 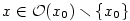 je je 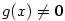 . Definujeme . Definujeme
-
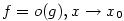 , jestliže , jestliže 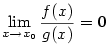 . .
-
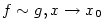 , jestliže , jestliže 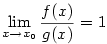 ;
říkáme, že ;
říkáme, že  je silně ekvivalentní s je silně ekvivalentní s 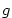 pro pro 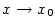 . .
|
Poznámka 7.16.
- Zápis
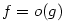 , , 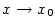 (čteme (čteme  je malé o je malé o 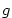 pro pro 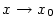 )
říká, že „funkce )
říká, že „funkce  je nekonečně malá vzhledem k funkci je nekonečně malá vzhledem k funkci 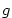 pro pro
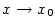 ”. ”.
- Zápis
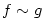 , , 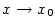 říká, že se funkce říká, že se funkce 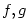 v okolí bodu v okolí bodu 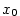 „chovají
přibližně stejně”. „chovají
přibližně stejně”.
- Má-li funkce
 v okolí v okolí 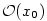 bodu bodu 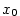 ohraničenou derivaci řádu ohraničenou derivaci řádu 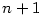 ,
vyplývá ze vztahu (7.5), že platí ,
vyplývá ze vztahu (7.5), že platí
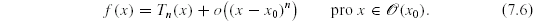
Lze ukázat, že dokonce stačí pouhá existence vlastní derivace 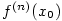 , tj. existence
Taylorova mnohočlenu , tj. existence
Taylorova mnohočlenu 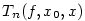 — viz [17, str. 175]).
Tedy pro zbytek v Taylorově vzorci dostáváme, že — viz [17, str. 175]).
Tedy pro zbytek v Taylorově vzorci dostáváme, že 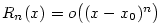 .
Tomuto tvaru zbytku se říká Peanův. .
Tomuto tvaru zbytku se říká Peanův.
|
| Příklad 7.18.
Vypočtěte limity

|
Řešení.
a) Nejprve si rozepíšeme Taylorovy vzorce funkcí 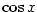 a a 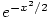 . Podle (7.6) platí: . Podle (7.6) platí:
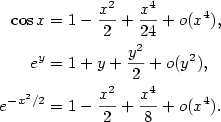
Dosazením do limity dostáváme
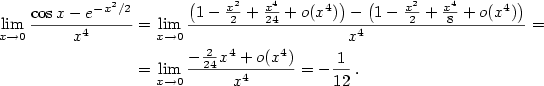
b) Opět si nejprve rozepíšeme Maclaurinovy vzorce funkcí v limitě:
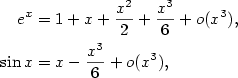
odkud
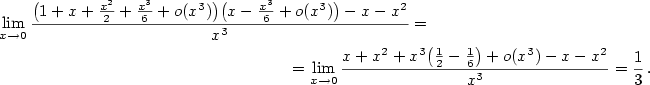
|
Zobrazit / skrýt řešení |
*
Matematici jsou jako Francouzi. Cokoliv jim řeknete, přeloží si do vlastního jazyka, čímž je z toho
něco úplně jiného.
(Johann Wolfgang von Goethe)
|
 v okolí daného bodu, tj. lokálně .
Zadanou funkci nahradíme (aproximujeme) nějakou jednodušší funkcí. V našem případě
budeme používat polynomy. Nejjednodušší aproximace je pomocí lineárního
polynomu, kdy přírůstek funkce zaměňujeme lineární funkcí — tzv. diferenciálem.
Aproximujeme-li funkci obecně polynomem stupně
v okolí daného bodu, tj. lokálně .
Zadanou funkci nahradíme (aproximujeme) nějakou jednodušší funkcí. V našem případě
budeme používat polynomy. Nejjednodušší aproximace je pomocí lineárního
polynomu, kdy přírůstek funkce zaměňujeme lineární funkcí — tzv. diferenciálem.
Aproximujeme-li funkci obecně polynomem stupně 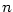 , mluvíme o Taylorově rozvoji.
, mluvíme o Taylorově rozvoji.
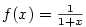 v okolí bodu
v okolí bodu 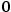 polynomem stupně
polynomem stupně 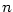 .
Použijeme vzorec pro součet nekonečné geometrické řady, podle kterého
.
Použijeme vzorec pro součet nekonečné geometrické řady, podle kterého

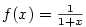 můžeme v okolí bodu
můžeme v okolí bodu 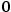 s určitou chybou nahradit funkcí
s určitou chybou nahradit funkcí
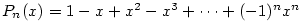 .
Říkáme, že funkci
.
Říkáme, že funkci  „lokálně
aproximujeme” (tj. nahrazujeme) polynomem stupně
„lokálně
aproximujeme” (tj. nahrazujeme) polynomem stupně 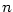 .
.
 je definovaná v okolí
je definovaná v okolí 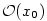 bodu
bodu 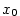 a platí
a platí 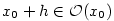 .
Pak číslo
.
Pak číslo 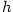 nazýváme přírůstkem nezávisle proměnné
a rozdíl
nazýváme přírůstkem nezávisle proměnné
a rozdíl 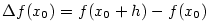 nazýváme přírůstkem funkce
nazýváme přírůstkem funkce  v bodě
v bodě 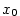 neboli přírůstkem závisle proměnné
— viz obr. 7.1.
neboli přírůstkem závisle proměnné
— viz obr. 7.1.
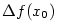 v závislosti na čísle
v závislosti na čísle 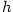 .
Nejjednodušší případ je obsahem následující definice.
.
Nejjednodušší případ je obsahem následující definice.
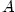 a funkce
a funkce 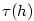 z definice 7.2 jsou určeny jednoznačně.
Nechť existuje diferenciál
z definice 7.2 jsou určeny jednoznačně.
Nechť existuje diferenciál 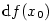 funkce
funkce  v bodě
v bodě 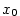 .
Snadno se ověří, že platí
.
Snadno se ověří, že platí
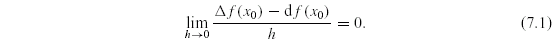
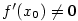 , platí rovněž
, platí rovněž


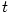 ke grafu funkce
ke grafu funkce  v bodě
v bodě 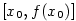 — viz obr. 7.1.
Pak platí
— viz obr. 7.1.
Pak platí 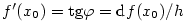 . Přírůstek
. Přírůstek 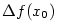 je součtem dvou hodnot:
diferenciálu
je součtem dvou hodnot:
diferenciálu 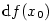 a
a 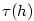 . Ze vztahů (7.1) a (7.2) je vidět, že pro malá
. Ze vztahů (7.1) a (7.2) je vidět, že pro malá 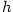 je (je-li
je (je-li 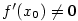 )
) 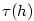 mnohem menší než diferenciál.
Nejběžnější aplikace diferenciálu spočívá v tom, že (pro malá
mnohem menší než diferenciál.
Nejběžnější aplikace diferenciálu spočívá v tom, že (pro malá 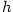 )
klademe
)
klademe
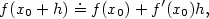
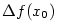 nahradíme s jistou chybou diferenciálem
nahradíme s jistou chybou diferenciálem
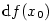 (geometricky graf funkce nahradíme její tečnou). Někdy se používá označení
(geometricky graf funkce nahradíme její tečnou). Někdy se používá označení
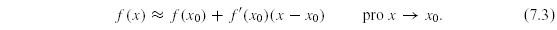
 má derivaci na množině
má derivaci na množině 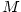 . Pak pro každé
. Pak pro každé 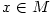 je definován
diferenciál
je definován
diferenciál 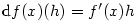 , tj. diferenciální funkce.
Je to funkce dvou proměnných: nezávislé proměnné
, tj. diferenciální funkce.
Je to funkce dvou proměnných: nezávislé proměnné 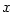 a přírůstku nezávisle proměnné
a přírůstku nezávisle proměnné 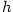 .
.
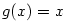 platí
platí 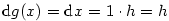 . Tato rovnost vysvětluje, proč
pro označení přírůstku nezávisle proměnné používáme rovněž symbol
. Tato rovnost vysvětluje, proč
pro označení přírůstku nezávisle proměnné používáme rovněž symbol 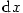 . Pro diferenciál funkce
. Pro diferenciál funkce  pak máme
pak máme 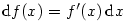 , odkud plyne
, odkud plyne 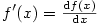 , což zdůvodňuje označení
pro derivaci funkce
, což zdůvodňuje označení
pro derivaci funkce  symbolem
symbolem 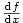 . Při tomto označení (pocházejícím od Leibnize,
označení čárkou zavedl Lagrange) mají některé vzorce pro derivování názorný tvar. Například:
. Při tomto označení (pocházejícím od Leibnize,
označení čárkou zavedl Lagrange) mají některé vzorce pro derivování názorný tvar. Například:
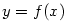 ,
, 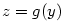 lze zapsat jako
lze zapsat jako
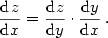
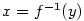 k funkci
k funkci 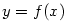 lze vyjádřit jako
lze vyjádřit jako
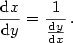
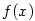 a hodnoty
a hodnoty 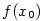 a
a 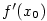 jsme
získali např. měřením. Zásadní význam má tento vztah rovněž
ve fyzice a pod. při odvozování nejrůznějších vzorců, kdy se vyšší
mocniny přírůstku (tj. u nás výraz
jsme
získali např. měřením. Zásadní význam má tento vztah rovněž
ve fyzice a pod. při odvozování nejrůznějších vzorců, kdy se vyšší
mocniny přírůstku (tj. u nás výraz 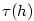 ) zanedbávají. Tyto členy vlastně zmizí při nějakém
limitním přechodu. Použití diferenciálu znamená linearizaci problému.
) zanedbávají. Tyto členy vlastně zmizí při nějakém
limitním přechodu. Použití diferenciálu znamená linearizaci problému.
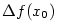 a relativní chyby
a relativní chyby 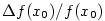 .
Klade se
.
Klade se 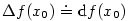 a
a 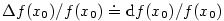 .
Toto použití ilustrují následující (velmi jednoduché) příklady.
.
Toto použití ilustrují následující (velmi jednoduché) příklady.
 v bodě
v bodě 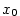 všechny derivace až do řádu
všechny derivace až do řádu 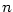 , které jsou vlastní.
Chceme funkci v okolí bodu
, které jsou vlastní.
Chceme funkci v okolí bodu 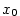 nahradit polynomem tvaru
nahradit polynomem tvaru 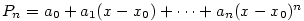 tak, aby polynom aproximoval funkci
tak, aby polynom aproximoval funkci  co „nejpřesněji”.
Je jistě rozumné požadovat, aby
co „nejpřesněji”.
Je jistě rozumné požadovat, aby

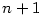 rovnic o neznámých
rovnic o neznámých 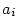 , kde
, kde 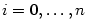 . Platí
. Platí
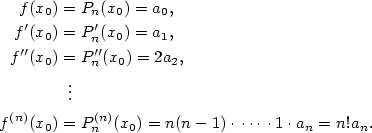
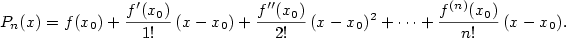
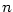 funkce
funkce  se středem
se středem 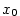 a značí se
a značí se
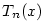 nebo podrobněji
nebo podrobněji 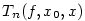 . Nahradíme-li funkci
. Nahradíme-li funkci  v okolí
bodu
v okolí
bodu 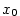 Taylorovým polynomem
Taylorovým polynomem 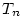 , dopustíme se chyby, kterou označujeme
, dopustíme se chyby, kterou označujeme 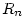 , tj.
, tj.
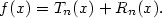
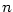 značí libovolné přirozené číslo a
značí libovolné přirozené číslo a 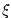 značí vhodné číslo
mezi
značí vhodné číslo
mezi 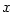 a nulou.
a nulou.
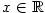 platí
platí
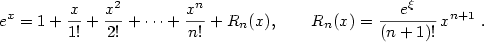
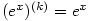 (důkaz provedeme indukcí), odkud
(důkaz provedeme indukcí), odkud 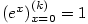 ,
, 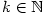 .
.
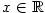 platí
platí
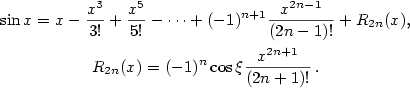
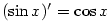 ,
, 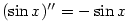 ,
,
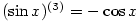 ,
, 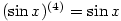 , odkud plyne pro
, odkud plyne pro 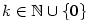
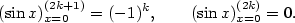
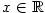 platí
platí
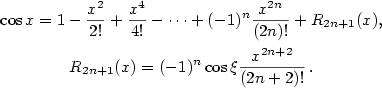
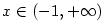 platí
platí

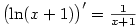 ,
, 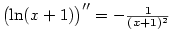 ,
obecně
,
obecně 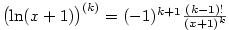 ,
tedy
,
tedy 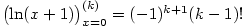 .
.
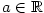 a
a 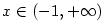 (v případě
(v případě 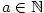 i pro
i pro 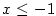 ) platí
) platí

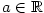 ,
, 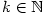 definujeme tzv. zobecněný binomický
koeficient
definujeme tzv. zobecněný binomický
koeficient
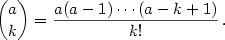
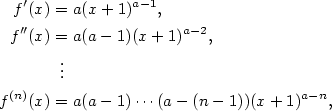
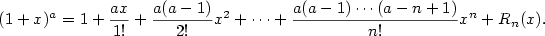
 ,
, 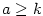 je definice zobecněného binomického koeficientu
ve shodě s definicí binomického čísla známou z elementární matematiky.
Speciálními případy binomického rozvoje jsou pro
je definice zobecněného binomického koeficientu
ve shodě s definicí binomického čísla známou z elementární matematiky.
Speciálními případy binomického rozvoje jsou pro 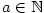 ,
, 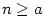 , binomická věta a pro
, binomická věta a pro
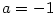 geometrická řada. Ověřte!
geometrická řada. Ověřte!
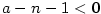 , pak pro každé
, pak pro každé 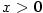 je odhad chyby
je odhad chyby
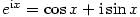 :
:
 jsou funkce,
jsou funkce, 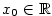 a nechť
existuje okolí
a nechť
existuje okolí 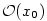 takové, že pro všechna
takové, že pro všechna 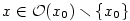 je
je 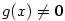 . Definujeme
. Definujeme
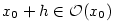 platí
platí
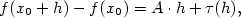
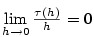 .
Je-li funkce
.
Je-li funkce 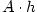 diferenciál funkce
diferenciál funkce 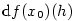 nebo stručně bez označení přírůstku
nebo stručně bez označení přírůstku 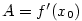 , a tedy
, a tedy
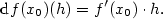
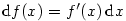 .)
.)
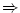 ”
” pro
pro  ,
,
 , kde
, kde
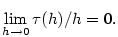 Odtud plyne
Odtud plyne
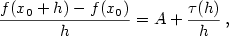
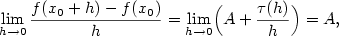
 ”
”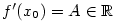 . Chceme dokázat, že
výraz
. Chceme dokázat, že
výraz 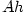 je diferenciál funkce
je diferenciál funkce 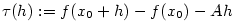 .
Pak
.
Pak
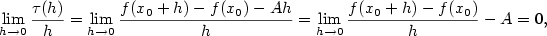
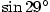 a
a  .
.
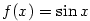 ,
, 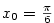 ,
, 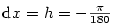 ,
,
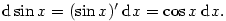
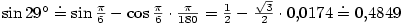 . Přesná hodnota je
po zaokrouhlení
. Přesná hodnota je
po zaokrouhlení 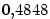 .
.
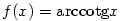 , diferenciál
, diferenciál
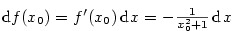 ,
, 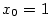 ,
, 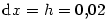 . S použitím diferenciálu dostaneme
. S použitím diferenciálu dostaneme
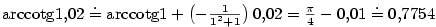 . Přesná hodnota je po zaokrouhlení
. Přesná hodnota je po zaokrouhlení 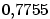 .
.
 platí
platí
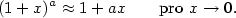
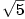 ,
, 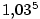 a
a 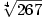 .
.
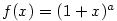 ,
, 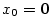 . Pak
. Pak 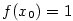 ,
, 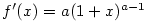 a
a 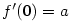 . Odtud máme
. Odtud máme
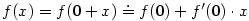 , tj.
, tj. 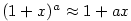 .
.
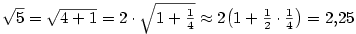 .
Můžeme ověřit, jak je naše aproximace přesná: Na kalkulačce najdeme (po zaokrouhlení)
.
Můžeme ověřit, jak je naše aproximace přesná: Na kalkulačce najdeme (po zaokrouhlení)
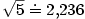 , a proto chyba, které jsme se aproximací dopustili, je
, a proto chyba, které jsme se aproximací dopustili, je 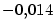 .
.
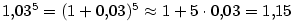 .
.
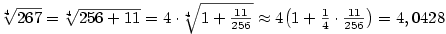 .
.
 vezmeme hodnotu
vezmeme hodnotu 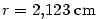 . Odhadněte relativní chybu výpočtu.
. Odhadněte relativní chybu výpočtu.
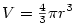 .
Platí
.
Platí 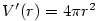 , a proto
, a proto
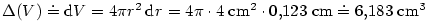 .
.
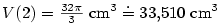 , tedy pro relativní chybu máme
, tedy pro relativní chybu máme
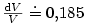 , tj. asi
, tj. asi  .
Nebo
.
Nebo 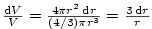 se stejným výsledkem.
se stejným výsledkem.
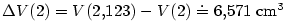 a
a
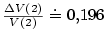 , tj. asi
, tj. asi 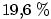 .
.
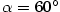 a poloměru
a poloměru 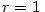 m
m
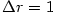 cm;
cm;
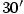 .
.
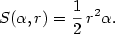
 v závislosti na
v závislosti na  . Aproximujeme
skutečný rozdíl
. Aproximujeme
skutečný rozdíl 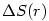 pomocí diferenciálu a dostáváme
pomocí diferenciálu a dostáváme
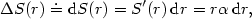
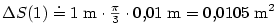 .
.
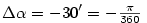 rad. Aproximujeme funkci
rad. Aproximujeme funkci 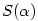 diferenciálem
diferenciálem
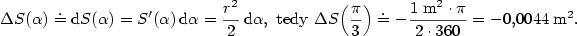
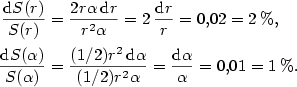
 .
Pak pro všechna
.
Pak pro všechna 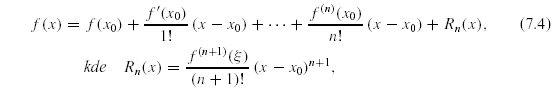
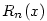 se
nazývá zbytek a vzorec
se
nazývá zbytek a vzorec 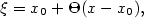
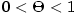 .
.
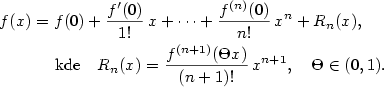
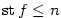 , pak
, pak  pro každé
pro každé  je nulový polynom.
je nulový polynom.
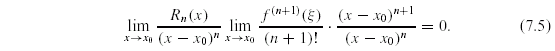
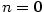 dostáváme
dostáváme 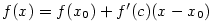 , což je Lagrangeova věta
o střední hodnotě;
, což je Lagrangeova věta
o střední hodnotě;
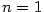 dostáváme vyjádření přírůstku funkce pomocí diferenciálu s chybou
dostáváme vyjádření přírůstku funkce pomocí diferenciálu s chybou
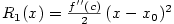 . Označíme-li
. Označíme-li 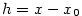 a
a 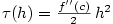 ,
dostáváme definici diferencovatelnosti funkce
,
dostáváme definici diferencovatelnosti funkce 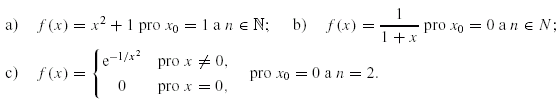
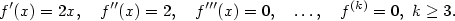
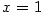 určíme hodnoty derivací a ze
určíme hodnoty derivací a ze 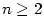 Taylorův polynom
Taylorův polynom
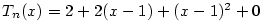 . Zřejmě
. Zřejmě 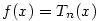 a
a 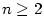 — viz
poznámka
— viz
poznámka  :
:
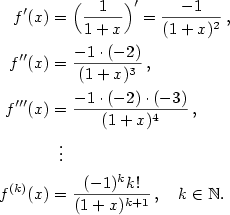
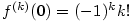 pro libovolné
pro libovolné  tvaru
tvaru
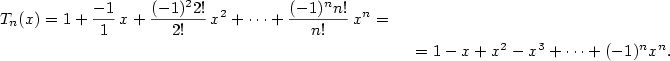
 spojitá. Spočítejme první derivaci v bodě
spojitá. Spočítejme první derivaci v bodě 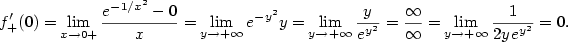
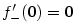 , dohromady
, dohromady 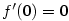 .
Druhou derivaci v bodě
.
Druhou derivaci v bodě 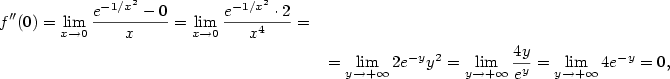
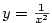 ) a dvakrát l'Hospitalovo pravidlo.
) a dvakrát l'Hospitalovo pravidlo.
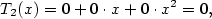
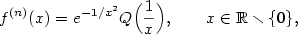
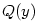 je polynom v proměnné
je polynom v proměnné 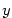 . Odtud
. Odtud 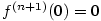 , neboť
, neboť
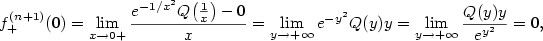
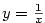 ) a poslední rovnost
zdůvodníme tím, že funkce
) a poslední rovnost
zdůvodníme tím, že funkce 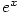 „utíká do nekonečna rychleji než libovolný polynom”.
Podobně vyjde
„utíká do nekonečna rychleji než libovolný polynom”.
Podobně vyjde 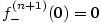 .
.
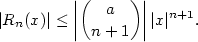
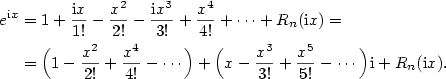
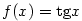 .
.
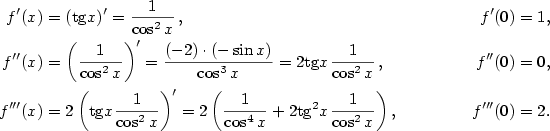
 v bodě
v bodě 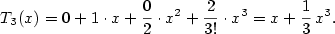
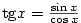 . Označme
. Označme 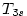 a
a 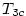 Taylorův polynom 3. stupně
funkcí po řadě
Taylorův polynom 3. stupně
funkcí po řadě 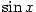 ,
, 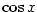 v bodě
v bodě 
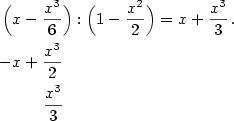
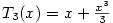 , ale podstatně jednodušší
cestou než v prvním případě. Tento postup lze korektně zdůvodnit — viz
, ale podstatně jednodušší
cestou než v prvním případě. Tento postup lze korektně zdůvodnit — viz 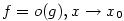 , jestliže
, jestliže 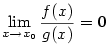 .
.
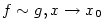 , jestliže
, jestliže 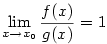 ;
říkáme, že
;
říkáme, že 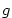 pro
pro 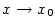 .
.
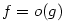 ,
, 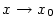 )
říká, že „funkce
)
říká, že „funkce 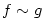 ,
, 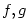 v okolí bodu
v okolí bodu 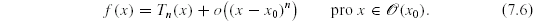
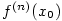 , tj. existence
Taylorova mnohočlenu
, tj. existence
Taylorova mnohočlenu 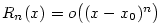 .
Tomuto tvaru zbytku se říká Peanův.
.
Tomuto tvaru zbytku se říká Peanův.
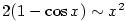 ,
, 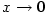 .
.
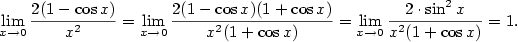

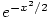 . Podle
. Podle 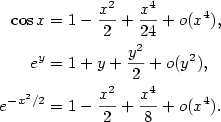
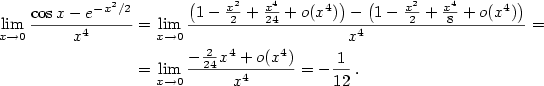
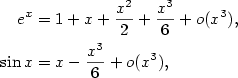
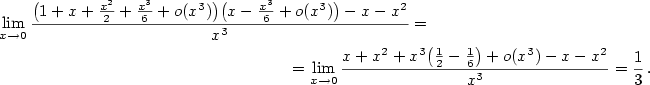
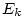 částice definována vztahem
částice definována vztahem
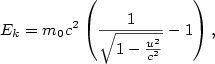
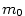 je klidová hmotnost částice,
je klidová hmotnost částice, 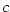 rychlost světla a
rychlost světla a 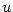 rychlost částice.
Ověřte, že je v tomto výrazu pro pohyby malou rychlostí
rychlost částice.
Ověřte, že je v tomto výrazu pro pohyby malou rychlostí 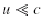 obsažen klasický vzorec
obsažen klasický vzorec
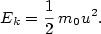
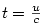 a
a 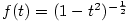 .
Vzorec pro
.
Vzorec pro 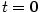 .
Z binomického rozvoje plyne
.
Z binomického rozvoje plyne
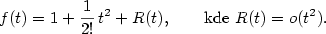
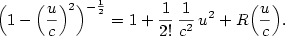
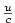 vystupovat ve vyšších mocninách,
a protože je
vystupovat ve vyšších mocninách,
a protože je 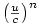 zanedbat.
Celkově pro
zanedbat.
Celkově pro