|
Věta 2.4 (Podílové kritérium - d'Alembertovo). Buď  řada s kladnými členy. řada s kladnými členy.
- Platí-li pro všechna
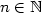 nerovnost nerovnost  , pak řada , pak řada  konverguje. Platí-li pro všechna konverguje. Platí-li pro všechna 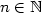 nerovnost nerovnost 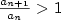 , pak řada , pak řada  diverguje. diverguje.
- Existuje-li
 , kde , kde  , ,
pak v případě  řada řada  konverguje a v případě konverguje a v případě  řada řada  diverguje. diverguje.
Poznámka 2.3. Tvrzení (ii) se nazývá limitní podílové kritérium. Je-li v tomto případě 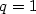 , nelze o konvergenci řady tímto kritériem rozhodnout. , nelze o konvergenci řady tímto kritériem rozhodnout.
Podobně jako odmocninové kritérium, také podílové kritérium vychází z geometrické řady

U geometrické řady je podíl sousedních dvou členů
 , ,
přitom řada je konvergentní (absolutně) pro  . .
Smyslem podílového kritéria je zjistit, zda se zkoumaná řada "limitně chová" jako konvergentní popř. divergentní geometrická řada.
| 




