|
Podstata odmocninového kritéria nemusí být na první pohled patrná. Toto kritérium se opírá o známou geometrickou řadu
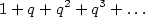
Tato řada je konvergentní (a to dokonce absolutně) pro  . Mějme nyní řadu s nezápornými členy . Mějme nyní řadu s nezápornými členy  a nechť platí a nechť platí 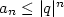 pro všechna pro všechna  . Odtud plyne . Odtud plyne
 . .
Odtud je již jen krůček ke zformulování následujícího kritéria.
Věta 2.3 (Odmocninové kritérium - Cauchyovo). Nechť  je řada s nezápornými členy. je řada s nezápornými členy.
- Platí-li pro všechna
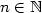 nerovnost nerovnost 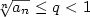 , pak řada konverguje. Platí-li pro nekonečně mnoho , pak řada konverguje. Platí-li pro nekonečně mnoho 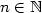 nerovnost nerovnost  , řada diverguje. , řada diverguje.
- Existuje-li
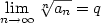 , kde , kde 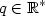 , ,
pak v případě  řada řada  konverguje a v případě konverguje a v případě  řada řada  diverguje. diverguje.
Poznámka 2.2. Tvrzení (ii) se nazývá limitní odmocninové kritérium. Je-li v tomto případě  , nelze o konvergenci řady tímto kritériem rozhodnout. , nelze o konvergenci řady tímto kritériem rozhodnout.
Konvergenci řady  tedy ověřujeme porovnáním s konvergentní geometrickou řadou. V limitním případě kontrolujeme, zda se naše řada "limitně chová" jako konvergentní popř. divergentní geometrická řada. tedy ověřujeme porovnáním s konvergentní geometrickou řadou. V limitním případě kontrolujeme, zda se naše řada "limitně chová" jako konvergentní popř. divergentní geometrická řada.
Připomeňme ještě, že na konvergenci číselné řady nemá vliv konečný počet jejích členů a proto můžeme předpoklady tvrzení (i) v tomto smyslu zeslabit.
| 




