Kapitola 5Derivace funkce
Derivace funkce patří spolu s pojmy limita a spojitost funkce k základním
pojmům diferenciálního počtu.
Nejprve si ukážeme historickou motivaci pro zavedení tohoto pojmu.
Poté dokážeme věty o derivaci, odvodíme derivace elementárních
funkcí a uvedeme věty o střední hodnotě popisující
vlastnosti funkce pomocí její derivace na intervalu.
Ukážeme, jak lze počítat limity podílu dvou funkcí
pomocí derivací – tzv. l'Hopitalovo pravidlo.
5.1. Derivace a její geometrický význam
K pojmu derivace funkce vede celá řada geometrických a fyzikálních úloh.
Jedna z nejstarších (tzv. základní úloha diferenciálního počtu) je nalézt
tečnu ke grafu
známé funkce  .
Sečna grafu je přímka
určená bodem .
Sečna grafu je přímka
určená bodem 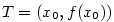 a dalším libovolným bodem grafu a dalším libovolným bodem grafu 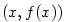 .
Tečnou s bodem dotyku .
Tečnou s bodem dotyku 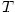 rozumíme limitní polohu zmíněné sečny, kdy se bod rozumíme limitní polohu zmíněné sečny, kdy se bod 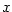 blíží k bodu blíží k bodu
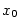 – viz obr. 5.1. Ukažme, jaká je směrnice této tečny. – viz obr. 5.1. Ukažme, jaká je směrnice této tečny.
Připomeňme, že přímka procházející body 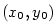 a a 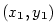 , , 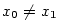 , má
směrnici , má
směrnici

kde 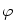 je úhel, který svírá přímka s kladným směrem osy je úhel, který svírá přímka s kladným směrem osy 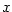 .
Tato přímka je potom dána rovnicí .
Tato přímka je potom dána rovnicí
 Proto směrnice uvažované sečny je
Proto směrnice uvažované sečny je
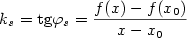
a směrnice tečny
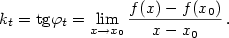
To ukazuje, že je účelné vyšetřovat takové limity (pro spojité funkce jsou typu 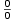 ). ).
Derivaci značíme též 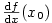 (důvodem je souvislost s diferenciálem,
viz kapitola 7) nebo
(důvodem je souvislost s diferenciálem,
viz kapitola 7) nebo 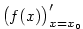 . .
Podobně definujeme jednostranné derivace
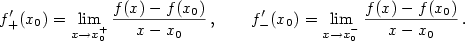
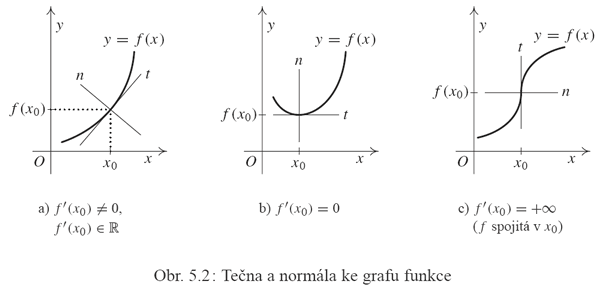
Geometrický význam derivace.
Ze způsobu, jakým jsme zavedli pojem derivace, plyne, že funkce  má v
bodě má v
bodě 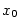 vlastní derivaci právě tehdy, když má graf v bodě vlastní derivaci právě tehdy, když má graf v bodě
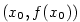 tečnu se směrnicí tečnu se směrnicí 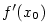 . Dosadíme-li do
(1), dostáváme rovnici této tečny v bodě . Dosadíme-li do
(1), dostáváme rovnici této tečny v bodě 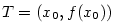
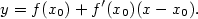
Pro směrnice 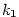 , , 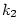 dvou navzájem kolmých přímek platí dvou navzájem kolmých přímek platí
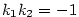 . Proto rovnice normály, tj. přímky kolmé k tečně a procházející
dotykovým bodem, je . Proto rovnice normály, tj. přímky kolmé k tečně a procházející
dotykovým bodem, je
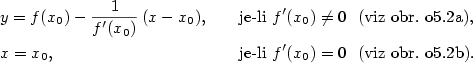
Má-li funkce v daném bodě nevlastní derivaci, tj. 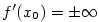 ,
a je-li v tomto bodě spojitá (viz poznámka 5.8, iii),
pak je tečna ke grafu funkce ,
a je-li v tomto bodě spojitá (viz poznámka 5.8, iii),
pak je tečna ke grafu funkce 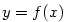 v bodě v bodě 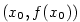 rovnoběžná s osou rovnoběžná s osou 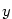 .
Proto rovnice tečny a normály tehdy jsou .
Proto rovnice tečny a normály tehdy jsou

Příklad 5.4.
Napište rovnici tečny a normály ke grafu funkce 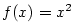 procházejících bodem procházejících bodem 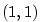 . .
|
Řešení.
Platí 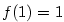 , takže půjde o bod dotyku.
Rovnice tečny má tvar , takže půjde o bod dotyku.
Rovnice tečny má tvar 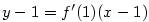 . Podle příkladu 5.3 je . Podle příkladu 5.3 je 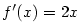 ,
po dosazení ,
po dosazení 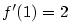 . Odtud dostáváme rovnici tečny . Odtud dostáváme rovnici tečny 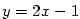 a normály a normály
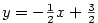 . . |
Zobrazit / skrýt řešení |
Příklad 5.5.
Rozhodněte, zda má funkce 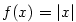 v bodě v bodě 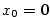 derivaci. derivaci.
|
Zobrazit / skrýt řešení |
Příklad 5.6. Z definice derivace vypočtěte derivace funkcí
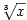 a a 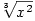 v bodě v bodě 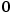 . .
|
Zobrazit / skrýt řešení |
Fyzikální význam derivace.
Předpokládejme, že v časovém intervalu 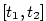 se po přímce pohybuje zleva doprava hmotný bod,
jehož poloha v čase se po přímce pohybuje zleva doprava hmotný bod,
jehož poloha v čase 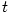 je určena souřadnicí je určena souřadnicí 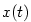 bodu dané přímky.
Průměrná rychlost v daném časovém intervalu je bodu dané přímky.
Průměrná rychlost v daném časovém intervalu je

Okamžitou rychlost 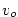 v nějakém čase v nějakém čase 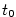 zjistíme tak, že
budeme „zmenšovat” velikost časového intervalu, tj. budeme se
„blížit k bodu zjistíme tak, že
budeme „zmenšovat” velikost časového intervalu, tj. budeme se
„blížit k bodu 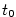 ”. Vyjádřeno matematicky pomocí limity ”. Vyjádřeno matematicky pomocí limity
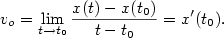
Vidíme, že fyzikální význam derivace je v tomto případě okamžitá rychlost hmotného bodu.
Podobně obecněji, jestliže 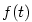 je fyzikální skalární veličina závisející na čase, charakterizuje je fyzikální skalární veličina závisející na čase, charakterizuje
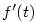 okamžitou velikost její změny v čase okamžitou velikost její změny v čase 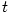 . .
5.2. Věty o derivaci
V tomto odstavci uvedeme věty o derivaci funkce v daném bodě. Vztah mezi
derivací a spojitostí funkce popisuje následující věta.
Věta 5.7.
Má-li funkce  v bodě v bodě 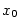 vlastní derivaci, pak je v tomto bodě spojitá. vlastní derivaci, pak je v tomto bodě spojitá.
|
Zobrazit / skrýt důkaz |
Věta 5.9.
Nechť mají funkce 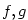 v bodě v bodě 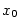 vlastní derivaci. Pak platí: vlastní derivaci. Pak platí:
-
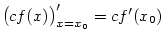 , ,
-
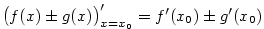 , ,
-
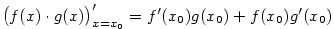 , ,
-
Je-li
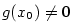 , pak , pak
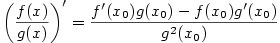 . .
|
Zobrazit / skrýt důkaz |
Před důkazem vět o derivaci složené a inverzní funkce uvedeme následující ekvivalentní
definici vlastní derivace, která nám umožní tyto věty elegantně dokázat.
| Poznámka 5.13.
Předchozí větu lze opět rozšířit i pro vícenásobně složené funkce.
Např. pro čtyřnásobně složenou funkci je:
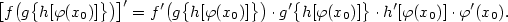
|
|
Obdobné tvrzení platí i pro jednostranné derivace.
Zobrazit / skrýt důkaz |
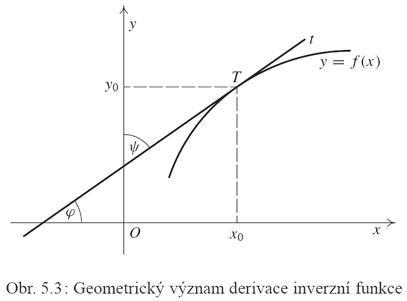
Tvrzení předchozí věty má názorný geometrický význam. Na obr. 5.3 platí pro
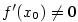 , že , že 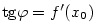 a a 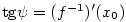 . Protože . Protože 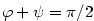 ,
platí ,
platí
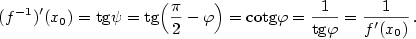
Pochopitelně tento obrázek nemůže nahradit výše uvedený korektní důkaz.
Protože podle poznámky 5.10 lze vlastní derivaci funkce  chápat jako funkci,
můžeme definovat její derivaci v nějakém bodě chápat jako funkci,
můžeme definovat její derivaci v nějakém bodě 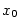 ; tu pak nazýváme druhou derivací
funkce ; tu pak nazýváme druhou derivací
funkce  v bodě v bodě 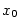 a značíme a značíme 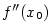 . Rovněž vlastní druhou derivaci lze chápat jako
funkci . Rovněž vlastní druhou derivaci lze chápat jako
funkci 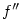 na množině na množině  . Ta může mít opět derivaci v některém bodě atd. . Ta může mít opět derivaci v některém bodě atd.
Obecně definujeme:
Definice 5.15.
Druhou derivací funkce  rozumíme funkci rozumíme funkci 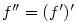 a pro libovolné a pro libovolné
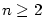 definujeme definujeme 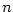 -tou derivaci
(derivaci -tou derivaci
(derivaci 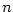 -tého řádu) funkce -tého řádu) funkce  vztahem vztahem 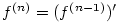 . .
|
Příklad 5.17.
Vypočtěte derivace všech řádů polynomu 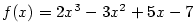 . .
|
Zobrazit / skrýt řešení |
5.3. Derivace elementárních funkcí
| Věta 5.18. Pro derivace elementárních funkcí platí:
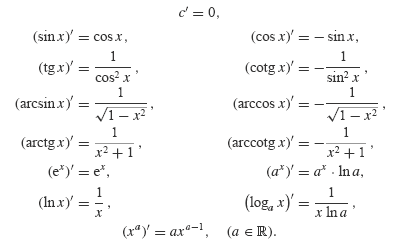
Tyto vzorce platí všude tam, kde jsou příslušné funkce definovány.
|
Zobrazit / skrýt důkaz |
Příklad 5.19. Vypočtěte derivace následujících funkcí:
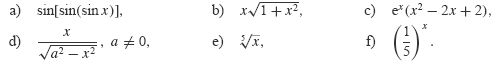
|
Řešení.
Vzhledem k předchozí větě platí:
-
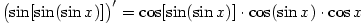 , ,
 , ,
-
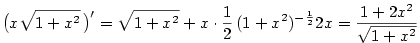 , ,  , ,
-
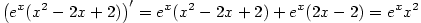 , , 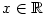 , ,
-
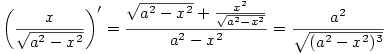 , , 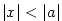 , ,
-
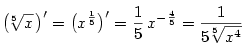 , , 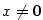 , ,
-
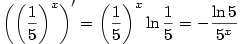 , , 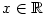 . .
|
Zobrazit / skrýt řešení |
5.4. Věty o střední hodnotě
Úvodem dokážeme jedno pomocné tvrzení.
Lemma 5.22.
Nechť 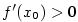 . Pak funkce . Pak funkce  je rostoucí v bodě je rostoucí v bodě 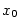 .
Analogicky, je-li .
Analogicky, je-li 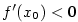 , je funkce , je funkce  klesající v bodě klesající v bodě 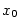 . .
|
Důkaz. Platí
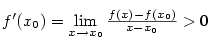 . Podle
věty 4.10 existuje okolí . Podle
věty 4.10 existuje okolí 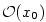 takové, že pro všechna takové, že pro všechna
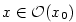 platí platí 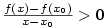 .
Podobně druhé tvrzení. .
Podobně druhé tvrzení.
|
Zobrazit / skrýt důkaz |
Všimněte si, že opačné tvrzení neplatí: Je-li funkce  je rostoucí v je rostoucí v 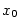 ,
nemusí být ,
nemusí být 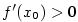 .
Například funkce .
Například funkce 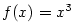 je rostoucí v je rostoucí v 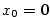 , ale , ale 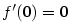 .
Následující tři věty se obvykle nazývají věty o střední hodnotě.
Připomeňme (definice 4.32), že .
Následující tři věty se obvykle nazývají věty o střední hodnotě.
Připomeňme (definice 4.32), že 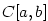 značí množinu všech
funkcí spojitých na intervalu značí množinu všech
funkcí spojitých na intervalu 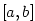 . .
Věta 5.23. (Rolleova věta)
Nechť funkce 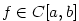 má v každém bodě intervalu má v každém bodě intervalu 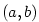 vlastní nebo nevlastní derivaci a nechť
vlastní nebo nevlastní derivaci a nechť 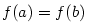 . Pak existuje . Pak existuje 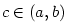 tak, že
tak, že 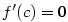 . .
|
Důkaz.
Je-li  na intervalu na intervalu 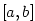 konstantní, je tvrzení zřejmé.
Nechť tedy existuje konstantní, je tvrzení zřejmé.
Nechť tedy existuje 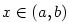 tak, že tak, že 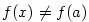 . Nechť např. . Nechť např.
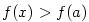 (pro (pro 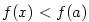 analogicky). Podle Weierstrassovy věty existuje analogicky). Podle Weierstrassovy věty existuje
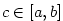 , v němž funkce , v němž funkce  nabývá své největší hodnoty nabývá své největší hodnoty 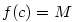 . Protože . Protože
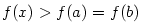 , je , je 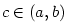 . Ukážeme, že . Ukážeme, že 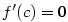 . Kdyby bylo . Kdyby bylo
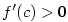 , pak by podle předcházejícího lemmatu 5.22 existovalo , pak by podle předcházejícího lemmatu 5.22 existovalo 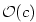 tak, že
pro tak, že
pro 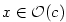 , , 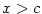 by platilo by platilo 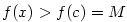 , což je spor. Analogicky
se ukáže, že nemůže být , což je spor. Analogicky
se ukáže, že nemůže být 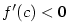 . .
|
Zobrazit / skrýt důkaz |
Důkaz.
Položme
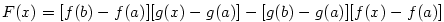 . Tato funkce . Tato funkce 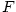 je spojitá
na je spojitá
na 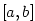 , má derivaci na , má derivaci na 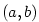 a platí a platí 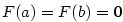 , tj. splňuje
předpoklady Rolleovy věty. Existuje tedy , tj. splňuje
předpoklady Rolleovy věty. Existuje tedy 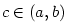 , pro které , pro které 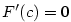 .
Přitom platí .
Přitom platí
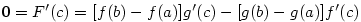 , odkud již tvrzení přímo plyne. , odkud již tvrzení přímo plyne.
|
Zobrazit / skrýt důkaz |
Důkaz.
Postupuje se analogicky jako v předcházející větě, kde se volí 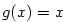 . .
|
Zobrazit / skrýt důkaz |

Geometrický význam.
Označme body roviny 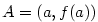 , , 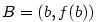 . Je-li . Je-li 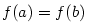 , Rolleova věta zaručuje
(za dalších předpokladů), že existuje alespoň jeden vnitřní bod , Rolleova věta zaručuje
(za dalších předpokladů), že existuje alespoň jeden vnitřní bod 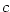 , v němž je derivace nulová,
tj. tečna ke grafu funkce , v němž je derivace nulová,
tj. tečna ke grafu funkce  v bodě v bodě 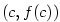 je rovnoběžná s osou je rovnoběžná s osou 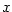 . Na obr. 5.4a
jsou takové body dva — . Na obr. 5.4a
jsou takové body dva — 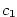 a a 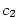 . .
Lagrangeova věta, která ji zobecňuje, pak říká, že
existuje alespoň jeden vnitřní bod 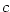 takový, že tečna v bodě takový, že tečna v bodě 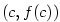 je rovnoběžná
s úsečkou je rovnoběžná
s úsečkou 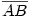 — viz obr. 5.4b. — viz obr. 5.4b.
I Cauchyovu větu lze znázornit obdobně na křivce dané parametricky,
Z Lagrangeovy věty vyplývá následující důležité tvrzení.
Důsledek 5.27.
Nechť funkce 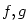 mají vlastní derivace v každém bodě otevřeného intervalu mají vlastní derivace v každém bodě otevřeného intervalu 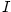 .
Jestliže pro všechna .
Jestliže pro všechna 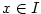 platí platí 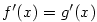 , pak
se funkce , pak
se funkce 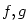 liší o konstantu, tj. existuje liší o konstantu, tj. existuje 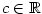 takové, že takové, že 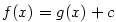 .
Zejména jestliže .
Zejména jestliže 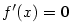 na na 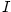 , je , je  na na 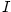 konstantní. konstantní.
|
Důkaz.
Mějme funkci 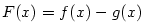 a body a body 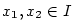 , , 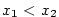 . Pak podle
Lagrangeovy věty existuje . Pak podle
Lagrangeovy věty existuje 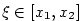 takové, že takové, že 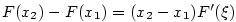 .
Přitom .
Přitom 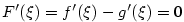 . Proto . Proto 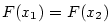 , tj. , tj. 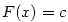 na na  , a tedy , a tedy
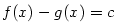 . .
|
Zobrazit / skrýt důkaz |
Tvrzení z důsledku 5.27 platí pro libovolný, ne jen otevřený interval,
pokud předpokládáme spojitost  a a 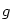 v krajních bodech.
V předchozím důsledku je podstatné, že v krajních bodech.
V předchozím důsledku je podstatné, že 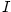 je interval. Např. pro funkci je interval. Např. pro funkci 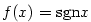 , ,
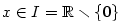 platí platí 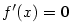 na na 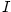 , ale tato funkce není na , ale tato funkce není na 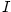 konstantní. konstantní.
Příklad 5.28.
Určete, pro která 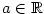 lze funkci lze funkci 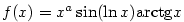 rozšířit na interval
rozšířit na interval 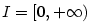 tak, aby výsledná
funkce tak, aby výsledná
funkce
a) byla spojitá na 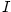 , , |
b) měla vlastní derivaci na 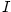 . . |
|
Zobrazit / skrýt řešení |
5.5. L'Hospitalovo pravidlo
Důkaz.
Dokážeme tvrzení např. pro limitu zprava. Důkaz pro limitu zleva je obdobný a jejich spojením
se vzhledem k větě 4.9 dostane oboustranný případ.
Označme 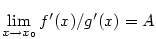 .
Nechť .
Nechť 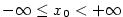 . Z předpokladů věty vyplývá existence čísla . Z předpokladů věty vyplývá existence čísla 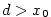 takového, že na intervalu
takového, že na intervalu 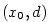 jsou funkce jsou funkce  a a 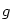 definované, jsou zde spojité a mají
zde vlastní derivaci, přičemž definované, jsou zde spojité a mají
zde vlastní derivaci, přičemž 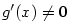 .
Navíc pro .
Navíc pro 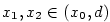 , , 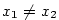 , je , je 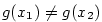 . (Jinak by podle Rolleovy
věty existovalo . (Jinak by podle Rolleovy
věty existovalo 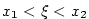 tak, že tak, že 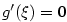 , což není možné.) , což není možné.)
Navíc je možné předpokládat, že i 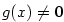 na intervalu na intervalu 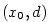 , kde totiž může existovat
nejvýše jedno , kde totiž může existovat
nejvýše jedno 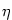 , v němž , v němž 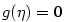 . Stačí tedy případně zmenšit . Stačí tedy případně zmenšit 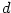 . .
Nechť nejprve 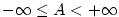 . Zvolme . Zvolme 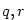 tak, aby tak, aby 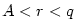 .
Z předpokladu o existenci limity .
Z předpokladu o existenci limity 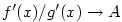 pro pro 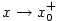 dostáváme, že existuje
dostáváme, že existuje 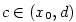 tak, že na intervalu tak, že na intervalu 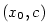 platí platí
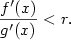
Pro libovolná 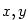 taková, že taková, že 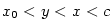 ,
existuje podle Cauchyovy věty o střední hodnotě číslo ,
existuje podle Cauchyovy věty o střední hodnotě číslo
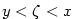 takové, že takové, že
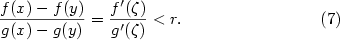
Nechť je splněna podmínka (i). Pak je 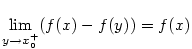 a obdobně je a obdobně je
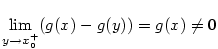 . Limitním přechodem . Limitním přechodem 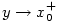 v \eqref{rLH1} dostaneme
(viz věta 4.10, 2), že pro libovolné v \eqref{rLH1} dostaneme
(viz věta 4.10, 2), že pro libovolné 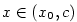 je je 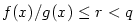 . .
Nechť je splněna podmínka (ii). Bez újmy na obecnosti můžeme předpokládat, že
např. 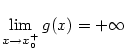 . (Ze spojitosti . (Ze spojitosti 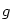 a faktu, že a faktu, že 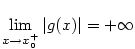 plyne, že v jistém pravém okolí bodu
plyne, že v jistém pravém okolí bodu 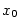 je funkce je funkce 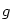 pořád kladná nebo pořád záporná.)
Zvolíme pevně pořád kladná nebo pořád záporná.)
Zvolíme pevně 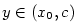 a najdeme a najdeme 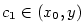 tak, aby platilo tak, aby platilo 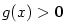 a a 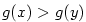 pro pro
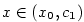 . Nyní vynásobíme část nerovnosti \eqref{rLH1} (v níž je zaměněno . Nyní vynásobíme část nerovnosti \eqref{rLH1} (v níž je zaměněno 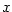 a a 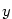 ) )
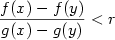
výrazem 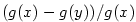 a dostaneme a dostaneme
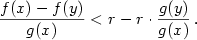
Odtud obdržíme
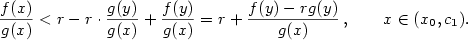
Nyní je s ohledem na podmínku (ii) možné najít 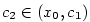 tak, že
na intervalu tak, že
na intervalu 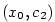 platí platí
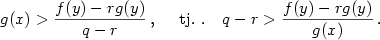
Spojením předchozích dvou nerovností opět dostáváme, že 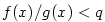 pro pro 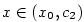 . .
V obou případech jsme dokázali, že v jistém pravém okolí bodu 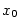 platí nerovnost platí nerovnost
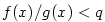 , kde , kde 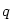 bylo libovolné číslo vyhovující nerovnosti bylo libovolné číslo vyhovující nerovnosti 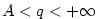 . .
Analogicky se dokáže, že v případě 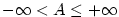 platí v jistém pravém okolí bodu platí v jistém pravém okolí bodu 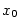 nerovnost
nerovnost 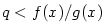 , kde , kde 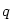 je libovolné číslo vyhovující nerovnosti je libovolné číslo vyhovující nerovnosti 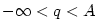 . .
Nyní již důkaz snadno dokončíme. Je-li 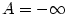 , vidíme přímo z definice nevlastní limity,
že , vidíme přímo z definice nevlastní limity,
že 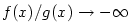 pro pro 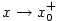 . Případ . Případ 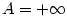 je obdobný. je obdobný.
Konečně je-li 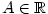 , zvolíme libovolné , zvolíme libovolné 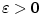 . V předchozích úvahách pak za . V předchozích úvahách pak za 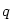 volíme
volíme 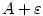 resp. resp. 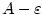 . V jistém pravém okolí bodu . V jistém pravém okolí bodu 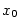 tedy platí nerovnost tedy platí nerovnost
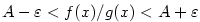 , což znamená, že , což znamená, že 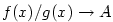 pro pro 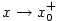 . .
|
Zobrazit / skrýt důkaz |
Příklad 5.31.
Vypočtěte následující limity:

|
Řešení.
- Limitu vypočítáme pomocí l'Hospitalova pravidla:
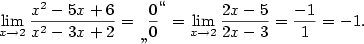
- Použijeme l'Hospitalovo pravidlo a vhodné úpravy:
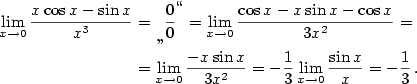
- Pro l'Hospitalovo pravidlo je typické vícenásobné použití. Dostaneme-li po derivování
opět limitu z podílu a jsou-li splněny předpoklady pro použití l'Hospitalova pravidla, zderivujeme
znovu čitatele a jmenovatele. Pokud vzniklá limita existuje, existuje i předchozí limita, a tudíž i
zadaná limita a všechny tři jsou si rovny. Tento postup je možné opakovat vícekrát.
V našem případě je:
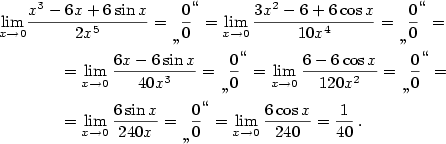
- Často vede k cíli, když po použití l'Hospitalova pravidla vhodně upravíme funkci na součin
a počítáme limity jednotlivých činitelů. V našem případě je:
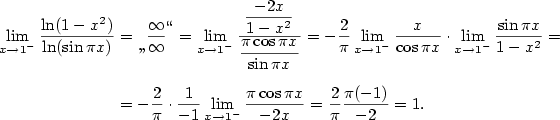
|
Zobrazit / skrýt řešení |
Neurčité výrazy.
Neurčitými výrazy rozumíme limitu součtu, součinu, rozdílu a podílu funkcí, v nichž limity jednotlivých
funkcí existují, ale příslušné operace s nimi nejsou definovány. Jde o tyto případy:
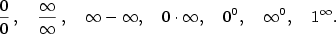
První dva případy limit lze řešit pomocí l'Hopitalova pravidla, další případy je možné
převést na první dva následovně.
-
Limita typu „
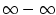 ”, tj. ”, tj. 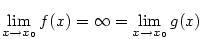 . Pak . Pak
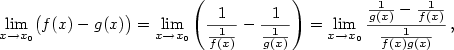
což je typ „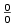 ”. ”.
-
Limita typu „
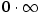 ”, tj. ”, tj. 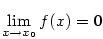 , ,
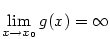 . Pak . Pak
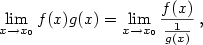
což je typ „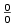 ”. ”.
-
Limity typu „
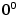 , , 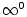 , , 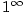 ”.
Řešíme úpravou na exponenciální funkci: ”.
Řešíme úpravou na exponenciální funkci:
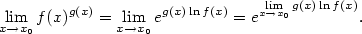
V poslední upravě jsme použili větu o limitě složené funkce 4.22, neboť
funkce 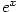 je spojitá. Pokud je limita v exponentu nevlastní, je třeba použít větu 4.16.
Přitom limita v exponentu je již typu „ je spojitá. Pokud je limita v exponentu nevlastní, je třeba použít větu 4.16.
Přitom limita v exponentu je již typu „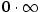 ”. ”.
Příklad 5.32. Vypočtěte následující limity:
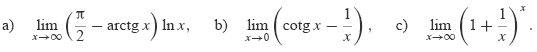
|
Řešení. Upravíme tak, abychom mohli použít l'Hopitalovo pravidlo.
- Součin převedeme na podíl:
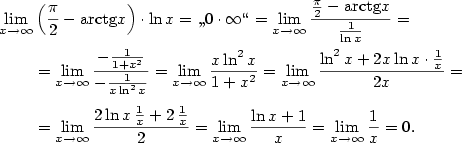
- Rozdíl převedeme na podíl:
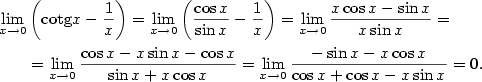
- Vyjádříme pomocí exponenciály:
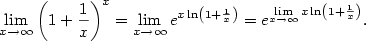
Počítejme zvlášť — součin převedeme na podíl:
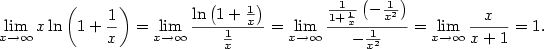
Původní limita je tedy 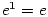 . .
|
Zobrazit / skrýt řešení |
L'Hospitalovo pravidlo lze využít i k výpočtu limit některých posloupností, nejčastěji
díky následujícímu tvrzení.
Věta 5.33.
Buď 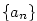 posloupnost a posloupnost a 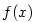 libovolná funkce taková, že libovolná funkce taková, že
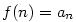 pro každé pro každé 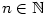 . Existuje-li . Existuje-li 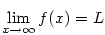 ,
pak existuje ,
pak existuje 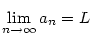 . .
|
| Důkaz.
Plyne snadno z definice limity v nevlastním bodě a limity posloupnosti.
Je rovněž speciálním případem tvrzení z věty D.15 dodatku.
|
Zobrazit / skrýt důkaz |
Příklad 5.34.
Pomocí předchozí věty určete 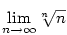 . .
|
Zobrazit / skrýt řešení |
5.6. Řešené příklady na derivaci a limitu
Příklad 5.35.
Vypočtěte následující derivace
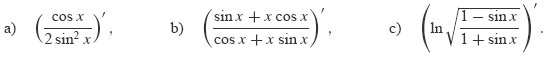
|
Zobrazit / skrýt řešení |
Příklad 5.36.
Vypočtěte derivaci
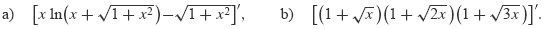
|
Zobrazit / skrýt řešení |
Následující příklady počítejte pomocí l'Hospitalova pravidla. Nezapomeňte vždy ověřit, zda jsou splněny
předpoklady pro jeho použití (typ „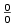 ”,
„ ”,
„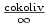 ”). ”).
Příklad 5.37.
Vypočítejte limity

|
Zobrazit / skrýt řešení |
Příklad 5.38.
Vypočítejte limity

|
Zobrazit / skrýt řešení |
|
 .
Sečna grafu je přímka
určená bodem
.
Sečna grafu je přímka
určená bodem 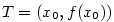 a dalším libovolným bodem grafu
a dalším libovolným bodem grafu 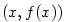 .
Tečnou s bodem dotyku
.
Tečnou s bodem dotyku 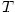 rozumíme limitní polohu zmíněné sečny, kdy se bod
rozumíme limitní polohu zmíněné sečny, kdy se bod 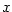 blíží k bodu
blíží k bodu
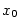 – viz obr. 5.1. Ukažme, jaká je směrnice této tečny.
– viz obr. 5.1. Ukažme, jaká je směrnice této tečny.
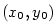 a
a 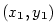 ,
, 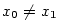 , má
směrnici
, má
směrnici

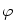 je úhel, který svírá přímka s kladným směrem osy
je úhel, který svírá přímka s kladným směrem osy 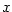 .
Tato přímka je potom dána rovnicí
.
Tato přímka je potom dána rovnicí
 Proto směrnice uvažované sečny je
Proto směrnice uvažované sečny je
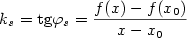
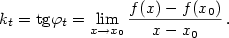
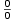 ).
).

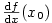 (důvodem je souvislost s diferenciálem,
viz kapitola 7) nebo
(důvodem je souvislost s diferenciálem,
viz kapitola 7) nebo 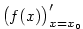 .
.
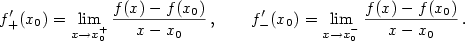
 má v
bodě
má v
bodě 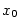 vlastní derivaci právě tehdy, když má graf v bodě
vlastní derivaci právě tehdy, když má graf v bodě
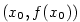 tečnu se směrnicí
tečnu se směrnicí 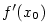 . Dosadíme-li do
(1), dostáváme rovnici této tečny v bodě
. Dosadíme-li do
(1), dostáváme rovnici této tečny v bodě 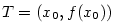
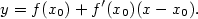
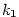 ,
, 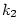 dvou navzájem kolmých přímek platí
dvou navzájem kolmých přímek platí
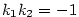 . Proto rovnice normály, tj. přímky kolmé k tečně a procházející
dotykovým bodem, je
. Proto rovnice normály, tj. přímky kolmé k tečně a procházející
dotykovým bodem, je
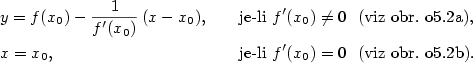
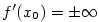 ,
a je-li v tomto bodě spojitá (viz poznámka 5.8, iii),
pak je tečna ke grafu funkce
,
a je-li v tomto bodě spojitá (viz poznámka 5.8, iii),
pak je tečna ke grafu funkce 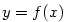 v bodě
v bodě 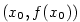 rovnoběžná s osou
rovnoběžná s osou 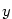 .
Proto rovnice tečny a normály tehdy jsou
.
Proto rovnice tečny a normály tehdy jsou


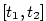 se po přímce pohybuje zleva doprava hmotný bod,
jehož poloha v čase
se po přímce pohybuje zleva doprava hmotný bod,
jehož poloha v čase 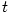 je určena souřadnicí
je určena souřadnicí 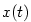 bodu dané přímky.
Průměrná rychlost v daném časovém intervalu je
bodu dané přímky.
Průměrná rychlost v daném časovém intervalu je

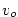 v nějakém čase
v nějakém čase 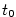 zjistíme tak, že
budeme „zmenšovat” velikost časového intervalu, tj. budeme se
„blížit k bodu
zjistíme tak, že
budeme „zmenšovat” velikost časového intervalu, tj. budeme se
„blížit k bodu 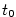 ”. Vyjádřeno matematicky pomocí limity
”. Vyjádřeno matematicky pomocí limity
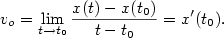
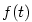 je fyzikální skalární veličina závisející na čase, charakterizuje
je fyzikální skalární veličina závisející na čase, charakterizuje
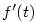 okamžitou velikost její změny v čase
okamžitou velikost její změny v čase 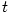 .
.
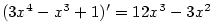 pro všechna
pro všechna 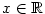 .
.

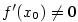 , že
, že 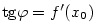 a
a 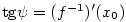 . Protože
. Protože 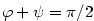 ,
platí
,
platí
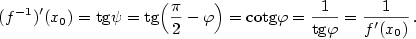
 chápat jako funkci,
můžeme definovat její derivaci v nějakém bodě
chápat jako funkci,
můžeme definovat její derivaci v nějakém bodě 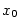 ; tu pak nazýváme druhou derivací
funkce
; tu pak nazýváme druhou derivací
funkce  v bodě
v bodě 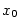 a značíme
a značíme 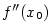 . Rovněž vlastní druhou derivaci lze chápat jako
funkci
. Rovněž vlastní druhou derivaci lze chápat jako
funkci 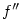 na množině
na množině 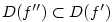 . Ta může mít opět derivaci v některém bodě atd.
. Ta může mít opět derivaci v některém bodě atd.
 rozumíme funkci
rozumíme funkci 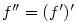 a pro libovolné
a pro libovolné
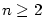 definujeme
definujeme 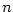 -tou derivaci
(derivaci
-tou derivaci
(derivaci 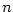 -tého řádu) funkce
-tého řádu) funkce  vztahem
vztahem 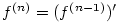 .
.
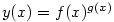 (tzv. „funkce na funkci”), kde
(tzv. „funkce na funkci”), kde 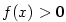 .
Úpravou na exponenciální funkci dostáváme
.
Úpravou na exponenciální funkci dostáváme
 je rostoucí v
je rostoucí v 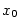 ,
nemusí být
,
nemusí být 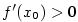 .
Například funkce
.
Například funkce 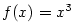 je rostoucí v
je rostoucí v 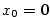 , ale
, ale 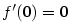 .
Následující tři věty se obvykle nazývají věty o střední hodnotě.
Připomeňme (definice 4.32), že
.
Následující tři věty se obvykle nazývají věty o střední hodnotě.
Připomeňme (definice 4.32), že 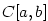 značí množinu všech
funkcí spojitých na intervalu
značí množinu všech
funkcí spojitých na intervalu 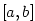 .
.

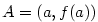 ,
, 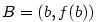 . Je-li
. Je-li 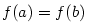 , Rolleova věta zaručuje
(za dalších předpokladů), že existuje alespoň jeden vnitřní bod
, Rolleova věta zaručuje
(za dalších předpokladů), že existuje alespoň jeden vnitřní bod 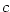 , v němž je derivace nulová,
tj. tečna ke grafu funkce
, v němž je derivace nulová,
tj. tečna ke grafu funkce  v bodě
v bodě 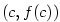 je rovnoběžná s osou
je rovnoběžná s osou 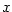 . Na obr. 5.4a
jsou takové body dva —
. Na obr. 5.4a
jsou takové body dva — 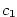 a
a 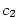 .
.
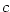 takový, že tečna v bodě
takový, že tečna v bodě 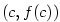 je rovnoběžná
s úsečkou
je rovnoběžná
s úsečkou 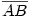 — viz obr. 5.4b.
— viz obr. 5.4b.
 a
a 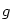 v krajních bodech.
V předchozím důsledku je podstatné, že
v krajních bodech.
V předchozím důsledku je podstatné, že 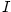 je interval. Např. pro funkci
je interval. Např. pro funkci 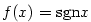 ,
,
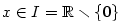 platí
platí 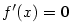 na
na 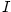 , ale tato funkce není na
, ale tato funkce není na 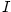 konstantní.
konstantní.
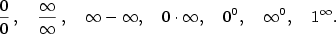
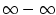 ”, tj.
”, tj. 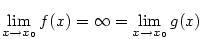 . Pak
. Pak
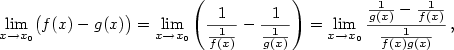
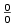 ”.
”.
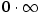 ”, tj.
”, tj. 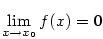 ,
,
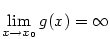 . Pak
. Pak
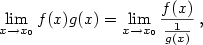
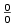 ”.
”.
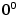 ,
, 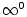 ,
, 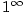 ”.
Řešíme úpravou na exponenciální funkci:
”.
Řešíme úpravou na exponenciální funkci:
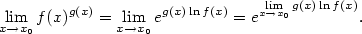
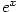 je spojitá. Pokud je limita v exponentu nevlastní, je třeba použít větu 4.16.
Přitom limita v exponentu je již typu „
je spojitá. Pokud je limita v exponentu nevlastní, je třeba použít větu 4.16.
Přitom limita v exponentu je již typu „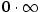 ”.
”.
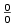 ”,
„
”,
„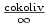 ”).
”).
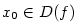 . Existuje-li
. Existuje-li

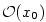 tak, že
tak, že 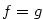 na
na 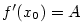 právě tehdy, když
právě tehdy, když 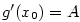 .
.
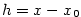 v
v 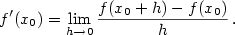
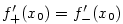 .
.
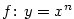 ,
, 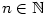 , v libovolném
bodě
, v libovolném
bodě 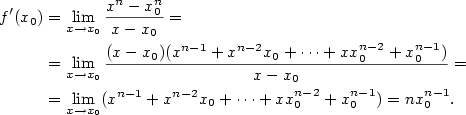
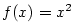 procházejících bodem
procházejících bodem 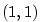 .
.
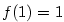 , takže půjde o bod dotyku.
Rovnice tečny má tvar
, takže půjde o bod dotyku.
Rovnice tečny má tvar 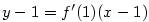 . Podle příkladu
. Podle příkladu 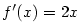 ,
po dosazení
,
po dosazení 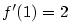 . Odtud dostáváme rovnici tečny
. Odtud dostáváme rovnici tečny 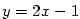 a normály
a normály
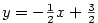 .
. 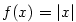 v bodě
v bodě 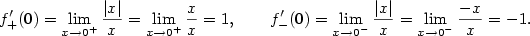
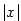 nemá derivaci v bodě
nemá derivaci v bodě 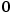 — viz. obr.
— viz. obr. 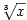 a
a 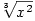 v bodě
v bodě 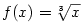 v bodě
v bodě 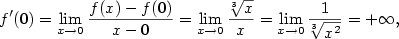
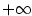 . Její tečnou je osa
. Její tečnou je osa 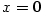 .
.
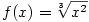 v bodě
v bodě 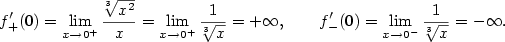
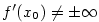 .
Podle definice spojitosti máme dokázat, že
.
Podle definice spojitosti máme dokázat, že 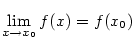 . Platí
. Platí
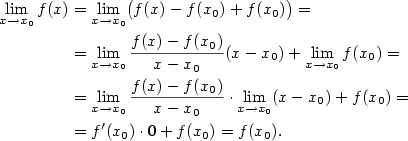
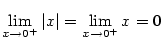 a
a 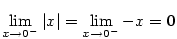 , ale
nemá v bodě
, ale
nemá v bodě 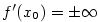 může (ale nemusí) být v bodě
může (ale nemusí) být v bodě 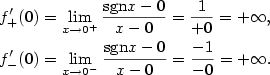
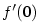 a je rovna
a je rovna 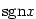 není v bodě
není v bodě  v bodě
v bodě 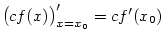 ,
,
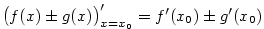 ,
,
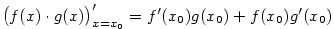 ,
,
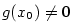 , pak
, pak
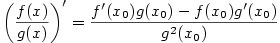 .
.
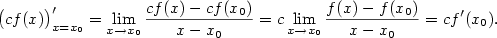
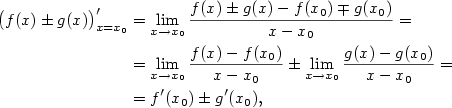
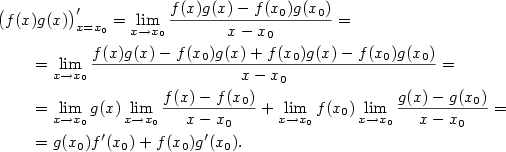
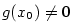 , proto
existuje okolí
, proto
existuje okolí 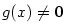 pro všechna
pro všechna 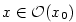 .
Podle definice derivace je
.
Podle definice derivace je
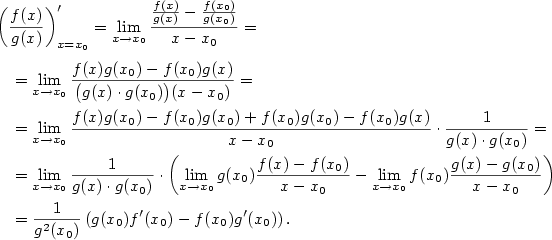
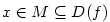 vlastní derivaci
vlastní derivaci
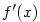 , pak
, pak 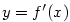 je funkce definovaná na
je funkce definovaná na 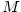 . Z předchozí věty plyne: Mají-li
funkce
. Z předchozí věty plyne: Mají-li
funkce 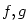 na množině
na množině 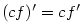 ,
, 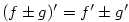 ,
, 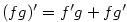 a pokud
a pokud 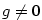 ,
, 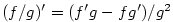 .
.
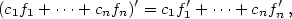
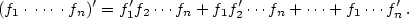
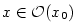 platí
platí
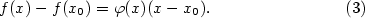
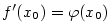 .
.
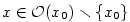 musí mít hledaná funkce
vzhledem k
musí mít hledaná funkce
vzhledem k 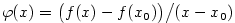 . Pro
. Pro 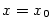 položíme
položíme
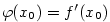 . Pak
. Pak
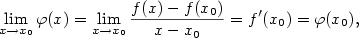
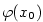 .
.
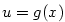 má vlastní derivaci v bodě
má vlastní derivaci v bodě 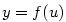 má vlastní derivaci v bodě
má vlastní derivaci v bodě 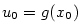 . Pak složená funkce
. Pak složená funkce 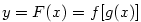 má vlastní derivaci v bodě
má vlastní derivaci v bodě 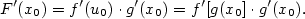
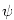 a
a 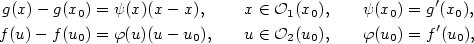
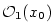 a
a 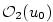 jsou vhodná okolí. Funkce
jsou vhodná okolí. Funkce 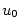 . Podle věty
. Podle věty 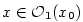 je
je 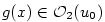 . Pak
. Pak
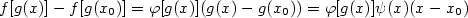
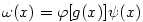 . Z vět
. Z vět 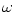 je spojitá v bodě
je spojitá v bodě 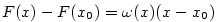 . Podle
lemmatu
. Podle
lemmatu 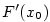 a je rovna
a je rovna
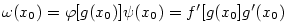 .
.
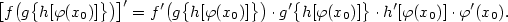
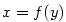 je spojitá a ryze monotonní na intervalu
je spojitá a ryze monotonní na intervalu 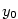 je vnitřní bod intervalu
je vnitřní bod intervalu 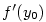 . Pak má inverzní funkce
. Pak má inverzní funkce 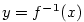 v bodě
v bodě 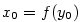 rovněž derivaci.
rovněž derivaci.
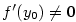 , je derivace inverzní funkce vlastní a platí
, je derivace inverzní funkce vlastní a platí
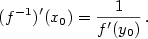
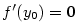 , je derivace inverzní funkce nevlastní, přičemž
, je derivace inverzní funkce nevlastní, přičemž 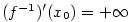 pro
pro 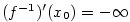 pro
pro 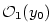 platí
platí
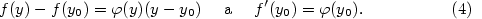
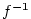 definovaná opět na intervalu a podle věty
definovaná opět na intervalu a podle věty 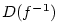 a existuje okolí
a existuje okolí
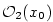 tak, že pro
tak, že pro
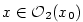 je
je 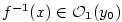 . Dosadíme-li
. Dosadíme-li 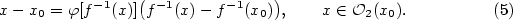
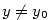 je
je
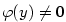 . Proto pro
. Proto pro 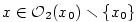 podle (5) platí
podle (5) platí
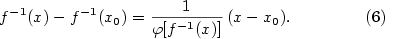
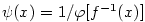 ,
, 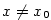 a položme
a položme 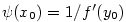 . Z vět
. Z vět 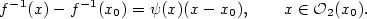
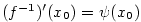 .
.
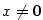 je podle (5)
je podle (5)
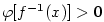 a podle věty
a podle věty 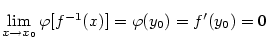 . Vzhledem k poznámce
. Vzhledem k poznámce 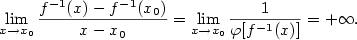
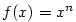 ,
, 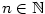 .
.
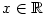
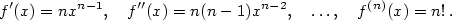
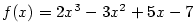 .
.
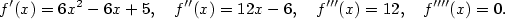
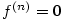 (nulový polynom) pro libovolné
(nulový polynom) pro libovolné 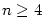 .
Všimněte si, že obdobnou vlastnost má každý polynom. Je-li
.
Všimněte si, že obdobnou vlastnost má každý polynom. Je-li 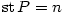 , pak
, pak
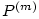 je nulový polynom pro každé
je nulový polynom pro každé 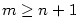 .
.
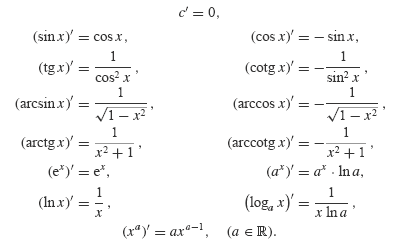
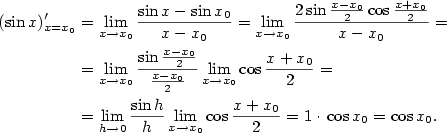
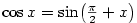 , plyne z věty o derivaci složené funkce
, plyne z věty o derivaci složené funkce
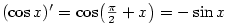 .
Derivaci funkce
.
Derivaci funkce 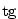 pak dostaneme z derivace podílu
pak dostaneme z derivace podílu 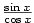 a derivaci
funkce
a derivaci
funkce 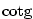 z derivace podílu
z derivace podílu 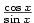 .
.
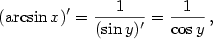
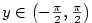 . Proto
. Proto 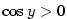 a
a
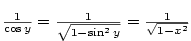 .
Podle příkladu
.
Podle příkladu 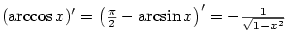 .
Podobně
.
Podobně
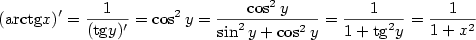
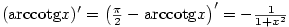 .
.
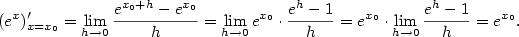
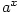 použijeme větu o složené funkci a dostáváme
použijeme větu o složené funkci a dostáváme
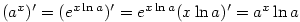 .
.
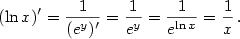
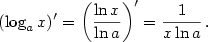
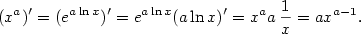
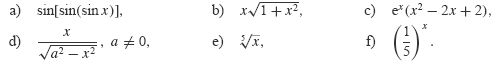
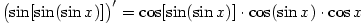 ,
,
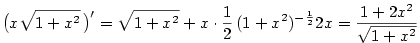 ,
, 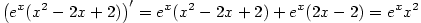 ,
, 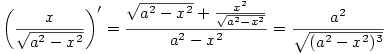 ,
, 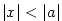 ,
,
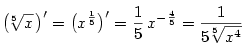 ,
, 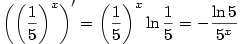 ,
, 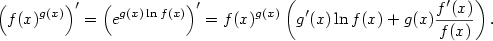
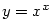 a
a 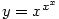 ,
, 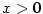 .
.
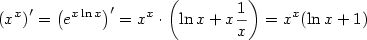
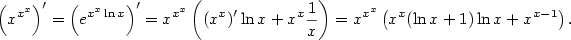
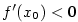 , je funkce
, je funkce 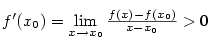 . Podle
věty
. Podle
věty 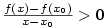 .
Podobně druhé tvrzení.
.
Podobně druhé tvrzení.
 má v každém bodě intervalu
má v každém bodě intervalu  vlastní nebo nevlastní derivaci a nechť
vlastní nebo nevlastní derivaci a nechť 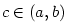 tak, že
tak, že 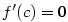 .
.
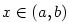 tak, že
tak, že 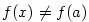 . Nechť např.
. Nechť např.
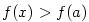 (pro
(pro 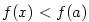 analogicky). Podle Weierstrassovy věty existuje
analogicky). Podle Weierstrassovy věty existuje
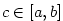 , v němž funkce
, v němž funkce 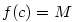 . Protože
. Protože
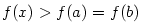 , je
, je 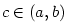 . Ukážeme, že
. Ukážeme, že 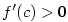 , pak by podle předcházejícího lemmatu
, pak by podle předcházejícího lemmatu 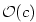 tak, že
pro
tak, že
pro 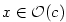 ,
, 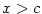 by platilo
by platilo 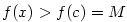 , což je spor. Analogicky
se ukáže, že nemůže být
, což je spor. Analogicky
se ukáže, že nemůže být 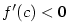 .
.
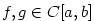 a nechť v každém bodě
a nechť v každém bodě 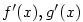 . Pak existuje
. Pak existuje 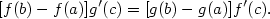
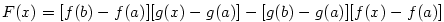 . Tato funkce
. Tato funkce 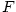 je spojitá
na
je spojitá
na 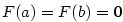 , tj. splňuje
předpoklady Rolleovy věty. Existuje tedy
, tj. splňuje
předpoklady Rolleovy věty. Existuje tedy 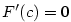 .
Přitom platí
.
Přitom platí
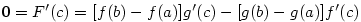 , odkud již tvrzení přímo plyne.
, odkud již tvrzení přímo plyne.
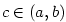 , pro které platí
, pro které platí
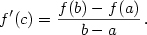
 .
.
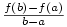 průměrná (střední) rychlost
v časovém intervalu
průměrná (střední) rychlost
v časovém intervalu 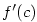 je okamžitá rychlost v čase
je okamžitá rychlost v čase 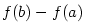 , jestliže dokážeme odhadnout
, jestliže dokážeme odhadnout
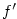 v intervalu
v intervalu 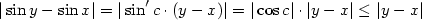
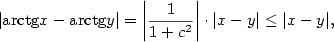
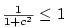 pro všechna
pro všechna 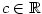 .
.
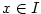 platí
platí 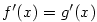 , pak
se funkce
, pak
se funkce 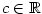 takové, že
takové, že 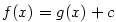 .
Zejména jestliže
.
Zejména jestliže 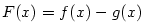 a body
a body 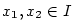 ,
, 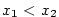 . Pak podle
Lagrangeovy věty existuje
. Pak podle
Lagrangeovy věty existuje 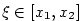 takové, že
takové, že 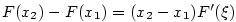 .
Přitom
.
Přitom 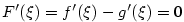 . Proto
. Proto 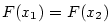 , tj.
, tj. 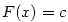 na
na 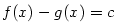 .
.
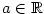 lze funkci
lze funkci 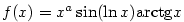 rozšířit na interval
rozšířit na interval 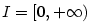 tak, aby výsledná
funkce
tak, aby výsledná
funkce
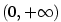 a má zde vlastní derivaci.
Problémový je tedy bod
a má zde vlastní derivaci.
Problémový je tedy bod 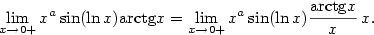
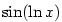 omezená na
omezená na 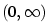 , ale její limita pro
, ale její limita pro 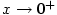 neexistuje
a
neexistuje
a 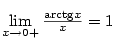 podle příkladu
podle příkladu 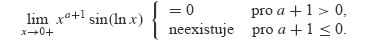
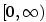 pouze pro
pouze pro 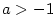 .
.
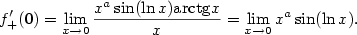
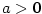 (a je rovna
(a je rovna 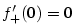 .
.
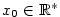 . Nechť je splněna jedna z podmínek
. Nechť je splněna jedna z podmínek
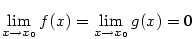 ,
,
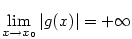 .
.
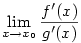 ,
pak existuje také
,
pak existuje také 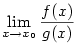 a platí
a platí
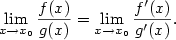
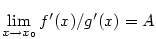 .
Nechť
.
Nechť 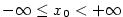 . Z předpokladů věty vyplývá existence čísla
. Z předpokladů věty vyplývá existence čísla 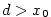 takového, že na intervalu
takového, že na intervalu 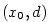 jsou funkce
jsou funkce 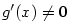 .
Navíc pro
.
Navíc pro 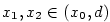 ,
, 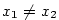 , je
, je 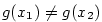 . (Jinak by podle Rolleovy
věty existovalo
. (Jinak by podle Rolleovy
věty existovalo 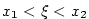 tak, že
tak, že 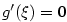 , což není možné.)
, což není možné.)
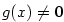 na intervalu
na intervalu 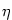 , v němž
, v němž 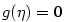 . Stačí tedy případně zmenšit
. Stačí tedy případně zmenšit 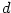 .
.
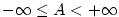 . Zvolme
. Zvolme 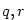 tak, aby
tak, aby 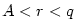 .
Z předpokladu o existenci limity
.
Z předpokladu o existenci limity 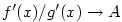 pro
pro 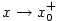 dostáváme, že existuje
dostáváme, že existuje 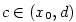 tak, že na intervalu
tak, že na intervalu 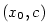 platí
platí
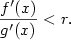
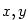 taková, že
taková, že 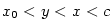 ,
existuje podle Cauchyovy věty o střední hodnotě číslo
,
existuje podle Cauchyovy věty o střední hodnotě číslo
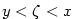 takové, že
takové, že
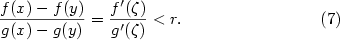
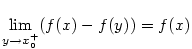 a obdobně je
a obdobně je
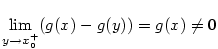 . Limitním přechodem
. Limitním přechodem 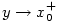 v \eqref{rLH1} dostaneme
(viz věta
v \eqref{rLH1} dostaneme
(viz věta 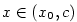 je
je 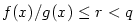 .
.
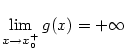 . (Ze spojitosti
. (Ze spojitosti 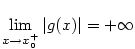 plyne, že v jistém pravém okolí bodu
plyne, že v jistém pravém okolí bodu 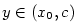 a najdeme
a najdeme 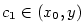 tak, aby platilo
tak, aby platilo 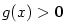 a
a 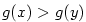 pro
pro
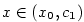 . Nyní vynásobíme část nerovnosti \eqref{rLH1} (v níž je zaměněno
. Nyní vynásobíme část nerovnosti \eqref{rLH1} (v níž je zaměněno 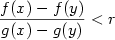
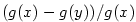 a dostaneme
a dostaneme
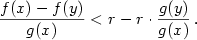
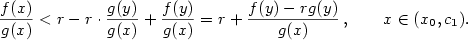
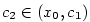 tak, že
na intervalu
tak, že
na intervalu 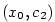 platí
platí
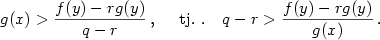
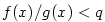 pro
pro 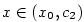 .
.
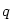 bylo libovolné číslo vyhovující nerovnosti
bylo libovolné číslo vyhovující nerovnosti 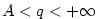 .
.
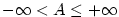 platí v jistém pravém okolí bodu
platí v jistém pravém okolí bodu 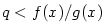 , kde
, kde 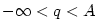 .
.
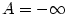 , vidíme přímo z definice nevlastní limity,
že
, vidíme přímo z definice nevlastní limity,
že 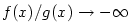 pro
pro 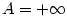 je obdobný.
je obdobný.
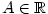 , zvolíme libovolné
, zvolíme libovolné 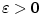 . V předchozích úvahách pak za
. V předchozích úvahách pak za 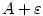 resp.
resp. 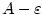 . V jistém pravém okolí bodu
. V jistém pravém okolí bodu 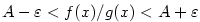 , což znamená, že
, což znamená, že 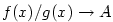 pro
pro 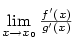 nemusí
existovat, což však neznamená, že neexistuje
nemusí
existovat, což však neznamená, že neexistuje 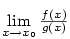 . Příkladem je
. Příkladem je
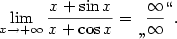
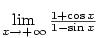 neexistuje.
Proto počítejme danou limitu jiným způsobem:
neexistuje.
Proto počítejme danou limitu jiným způsobem:
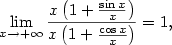
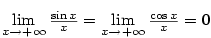 .
.
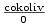 . Je důležité,
aby limita čitatele i jmenovatele byla
. Je důležité,
aby limita čitatele i jmenovatele byla 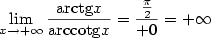
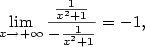

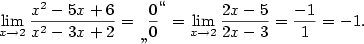
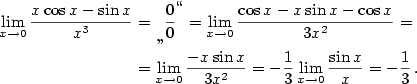
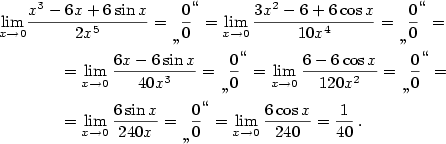
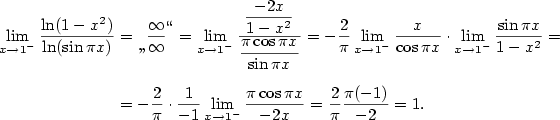
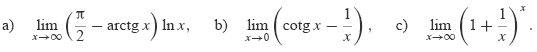
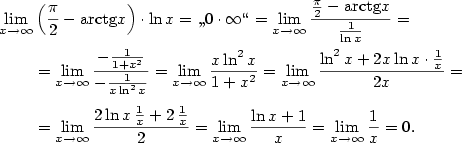
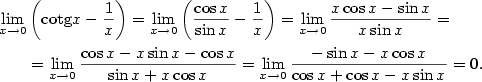
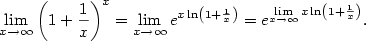
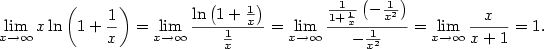
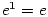 .
.
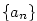 posloupnost a
posloupnost a 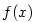 libovolná funkce taková, že
libovolná funkce taková, že
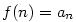 pro každé
pro každé 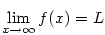 ,
pak existuje
,
pak existuje 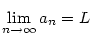 .
.
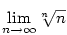 .
.
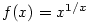 ,
, 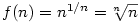 pro
pro 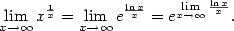
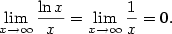
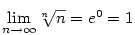 .
.
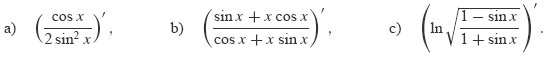
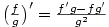 .
Platí
.
Platí
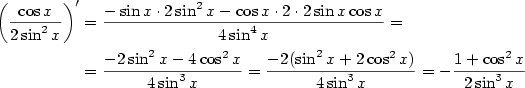
 , kde
, kde  .
b) Opět použijeme větu o derivaci podílu a upravíme.
Dostáváme
.
b) Opět použijeme větu o derivaci podílu a upravíme.
Dostáváme
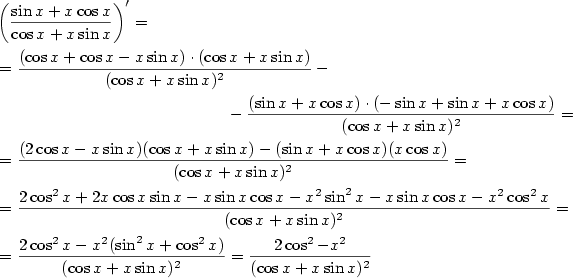
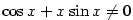 .
c) Použijeme větu o derivaci složené funkce a větu o derivaci podílu. Je
.
c) Použijeme větu o derivaci složené funkce a větu o derivaci podílu. Je
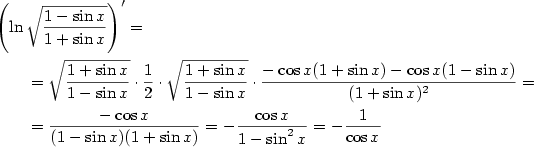
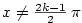 , kde
, kde 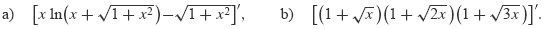
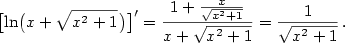
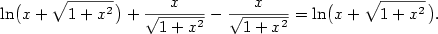
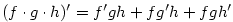 . V našem případě bude
. V našem případě bude
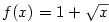 ,
, 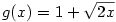 ,
, 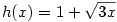 .
Dostáváme
.
Dostáváme
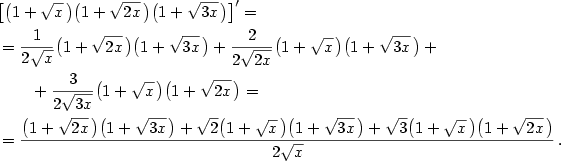

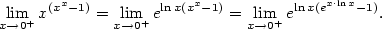
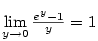 ,
,
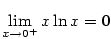 .
Dostáváme
.
Dostáváme
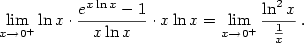
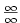 ):
):
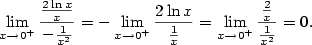
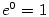 .
b) Jde o neurčitý výraz exponenciálního typu.
Proto nejprve provedeme úpravu
.
b) Jde o neurčitý výraz exponenciálního typu.
Proto nejprve provedeme úpravu
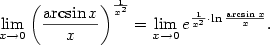
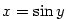 a využijeme znalosti
a využijeme znalosti
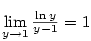 .
Dostáváme
.
Dostáváme
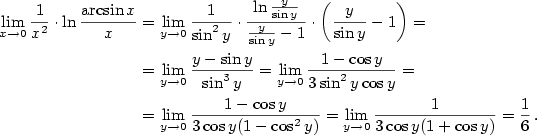
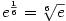 .
.

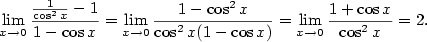
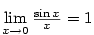 a poté použijeme
l'Hospitalovo pravidlo (typ
a poté použijeme
l'Hospitalovo pravidlo (typ