Interní reprezentace a substituce
1 Interní reprezentace
| (%i1) | pol: x^4+x^3-x^2-x; |
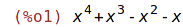
| (%i2) | op(pol); |
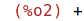
Pomocí nterms získáme počet sčítanců.
| (%i3) | nterms(pol); |

| (%i4) | length(pol); |

| (%i5) | inpart(pol,0); |

Vrací operátor (stejně jako příkaz op).
| (%i6) | inpart(pol,4); |
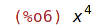
| (%i7) | part(pol,4); |
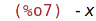
part a inpart vracejí podvýrazy daného výrazu, přičemž inpart se zaměřuje na
interní reprezentaci výrazu (ta může být odlišná od té zobrazené).
| (%i8) | inpart(pol,4,1);inpart(pol,4,2); |

| (%i10) | [part(pol,0), part(pol,1), part(pol,2), part(pol,3), part(pol,4)]; |
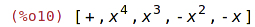
| (%i11) | dpart(pol,2); |
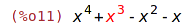
Označuje podvýraz.
| (%i12) | listofvars(pol); |
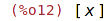
| (%i13) | dispform(pol); |
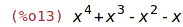
Vrací seznam proměnných, obsažených v zadaném výrazu.
| (%i14) | nterms(pol); |
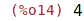
| (%i15) | op(pol); |
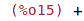
| (%i16) | op(x^4); |
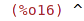
| (%i17) | op(-x^2); |
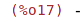
| (%i18) | op(x^2*y^3*z^4); |

| (%i19) | r: (y^2-1)/(y-1); |
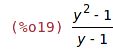
| (%i20) | op(r); |

| (%i21) | r:(sin(x)^2-1)/(sin(x)-1); |
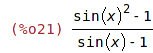
| (%i22) | op(r); |
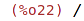
| (%i23) | rat(r); |
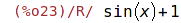
2 Substituce
Substituce se provádí příkazem subst(a,b,c), který má tři povinné parametry.
Nahrazuje b pomocí a ve výrazu c.
| (%i24) | subst(0,x, cos(x)*(sin(x)+x^2+1)); |
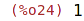
Subst je čistě syntaktická substituce, a, b musí být buď proměnné nebo
kompletní podvýrazy.
Ekvivalentí zápis je i tento
| (%i25) | subst(x=0, cos(x)*(sin(x)+x^2+1)); |
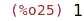
a tento
| (%i26) | cos(x)*(sin(x)+x^2+1), x=0; |
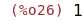
| (%i27) | expression:1+tan(x)^2; |

| (%i28) | subst(sin(x)/cos(x),tan(x), expression); |
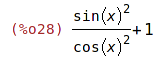
| (%i29) | subst(1-cos(x)^2,sin(x)^2,%); |
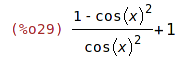
| (%i30) | ratsimp(%); |
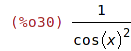
Posloupnost substitucí - program provede první substituci a ve výsledku pak další
substituci. Substituce píšeme do hranatých závorek a oddělujeme je čárkou.
V tomto případě můžeme použít pouze zápis s rovnítkem.
| (%i31) | subst([tan(x)=sin(x)/cos(x), sin(x)^2=1-cos(x)^2], expression); |
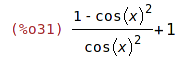
| (%i32) | ratsimp(%); |
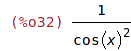
Paralelní posloupnost substitucí provádí příkaz psubst:
| (%i33) | psubst ([a^2=b, b=a], sin(a^2) + sin(b)); |
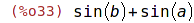
| (%i34) | subst ([a^2=b, b=a], sin(a^2) + sin(b)); |
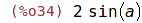
Paralelní (současná) substituce:
| (%i35) | psubst([x=y, y=z], x*y^2); |

Posloupnost substitucí:
| (%i36) | subst([x=y, y=z], x*y^2); |
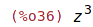
| (%i37) | subst([a=b, b=c, c=a], a+2*b+3*c); |
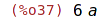
| (%i38) | psubst([a=b, b=c, c=a], a+2*b+3*c); |
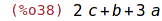
| (%i39) | subst(x+1=y, 3*(x+1)^2+x+1); |
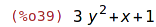
V tomto případě se syntaktická substituce neprovedla,
použijeme příkaz ratsubst, který si všímá matematického významu výrazu.
| (%i40) | ratsubst(y,x+1,3*(x+1)^2+x+1); |
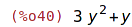
Zde je možné použít pouze tento typ zápisu.
| (%i41) | subst([a=b, b=c, c=a], a+2*b+3*c); |
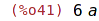
| (%i42) | load("lrats"); |
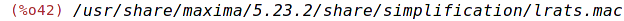
| (%i43) | lratsubst([a=b, b=c, c=a], a+2*b+3*c); |
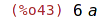
| (%i44) | fullratsubst([a=b, b=c, c=a], a+2*b+3*c); |
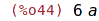
Lze provádět substituce i za části výrazů. Podmínkou je, že Maxima
interně rozezná podvýraz (výstup procedury part).
| (%i45) | expr1:x*y+z; expr2:x*y*z; expr3:(x*y)^2; |

| (%i48) | subst(soucin,x*y, expr1); |
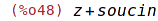
| (%i49) | subst(soucin,x*y, expr2); |

| (%i50) | subst(soucin,x*y, expr3); |
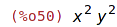
| (%i51) | length(expr1); |

| (%i52) | [part(expr1,1), part(expr1,2)]; |
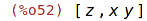
| (%i53) | length(expr2); |
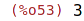
| (%i54) | [part(expr2,1),part(expr2,2),part(expr2,3)]; |
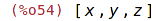
| (%i55) | length(expr3); |
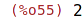
| (%i56) | [part(expr3,1),part(expr3,2)]; |
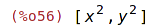
Ratsubst (narozdíl od subst) si všímá i matematického významu výrazu.
| (%i57) | ratsubst(soucin,x*y, expr2); |
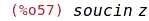
| (%i58) | ratsubst(soucin,x*y, expr3); |

| (%i59) | vyraz:a+b+c; |
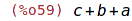
| (%i60) | subst(d,a+b, vyraz); |
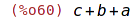
| (%i61) | ratsubst(d,a+b, vyraz); |
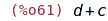
| (%i62) | p:a+2*b+3*c; |
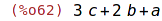
| (%i63) | ratsubst(d,a+b,p); |
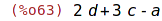
Pro substituci za operandy výrazu můžeme použít příkaz substpart.
| (%i64) | vyraz : x^2+x+1/x; |
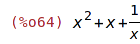
| (%i65) | substpart(y,vyraz,3); |
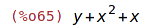
Třetí operand byl nahrazen y.
Opsubs provádí substituci pouze za operátory.
| (%i66) | load ("opsubst"); |
| (%i67) | opsubst(f,g,g(g(x))); |
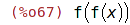
| (%i68) | opsubst([f=g,g=h],f(x)); |

Použití substitucí při úpravách výrazů.
| (%i69) | soucin:(x^2+y^2+2*x*y) * ((x+y)^2+1); |
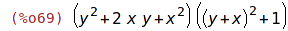
| (%i70) | factor(soucin); |
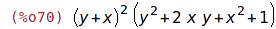
| (%i71) | substpart(factor(part(soucin,1)),soucin,1); |
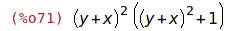
Zjednodušení z předcházejícího příkladu je možné provést i takto:
| (%i72) | subst(x+y=z, soucin); |
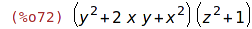
| (%i73) | factor(%); |
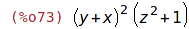
| (%i74) | subst(z=x+y, %); |
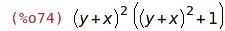
| (%i75) | vyraz:(x^2+2*x+1)^2+(x^2-2*x+1)^2; |
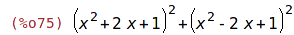
| (%i76) | factor(vyraz); |
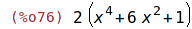
| (%i77) | map(factor, vyraz); |
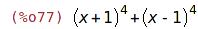
Substitucí často používáme při zjednodušování výrazů
| (%i78) | vyraz:(x+y)^2+1/(x+y)^2; |
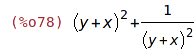
| (%i79) | rat(vyraz); |
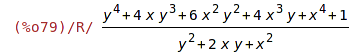
Chceme výraz transformovat na tvar čitatel/jmenovatel bez expanze (x+y)^2.
Dočasně nahradíme x+y pomocí např. z, použijeme příkaz rat a konečně provedeme
zpětnou substituci.
| (%i80) | subst(x+y=z, vyraz); |

| (%i81) | rat(%); |

| (%i82) | subst(z=x+y,%); |