Úvod do programování
1 Základní programové konstrukce
for variable: initial_value step increment thru limit do body
initial_value, increment, limit, a body mohou být libovolné výrazy.
| (%i1) | for i:1 thru 5 step 1 do display(i)$ |
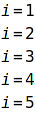
| (%i2) | i; |
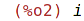
Pokud je přírůstek jedna může se step vynechat.
| (%i3) | for i:1 thru 5 do print(i)$ |
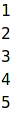
| (%i4) | total : 0; |

| (%i5) | for i:1 thru 5 do total : total +i$ |
| (%i6) | total; |
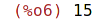
| (%i7) | for i:2 thru 6 step 2 do print('sum(j^i,j,1,n))$ |
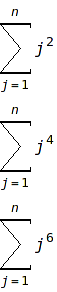
| (%i8) | i; |

| (%i9) | seznam : [1,2,3,4,5]; |
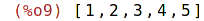
| (%i10) | s:0; |

| (%i11) |
for i:1 thru length(seznam) do if remainder(seznam[i],2)=0 then s:s+seznam[i]^2; |
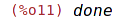
| (%i12) | print("soucet ctvercu s = ", s); |
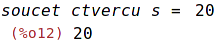
for variable in list end_tests do body
| (%i13) | kill(all); |
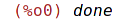
| (%i1) | s:0;seznam : [1,2,3,4,5]; |
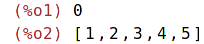
| (%i3) |
for i in seznam do if remainder(seznam[i],2)=0 then s:s+seznam[i]^2; |
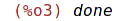
| (%i4) | print("soucet ctvercu s = ", s); |
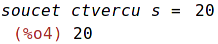
for variable: initial_value step increment while condition do body
| (%i5) | s : 0$ |
| (%i6) | for i:1 while i<=10 do s:s+i; |
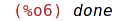
| (%i7) | s; |
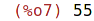
while ... do ... (unless ... do ...)
while provadi opakovane posloupnosti prikazu tak dlouho, pokud je podminka splnena
(tedy pokud je logicky vyraz typu true). Pokud ma podminka hned na zacatku hodnotu false,
posloupnost prikazu se neprovede.
| (%i8) | x : 256; |
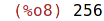
| (%i9) | while x>1 do x: x/4; |
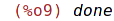
| (%i10) | x; |

| (%i11) | x : 1/2; |

| (%i12) | while x>1 do x: x/4; |
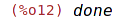
| (%i13) | x; |

Eukliduv algoritmus
| (%i14) |
a:20$ b:12$ while notequal(b,0) do ( d:remainder(a,b), a:b, b:d)$ |
| (%i17) | print("celociselny NSD je", a); |
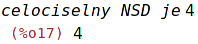
| (%i18) | gcd(20,12); |

| (%i19) | kill(all); |
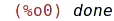
block([x1,x2,...,xn],exp1,exp2,...,expn)
Posloupnost příkazů, která se navenek chová jako jeden příkazů.
[x1,x2,...,xn] je posloupnost lokálních proměnných. Výsledem je výsledek posledního příkazu posloupnosti.
Block příkazů může být ukončen i pomocí return(x), x bude poté výsledkem bloku.
| (%i1) |
euklid(a,b):= block([],local(d),d:remainder(a,b), while notequal(d,0) do (a:b, b:d, d:remainder(a,b)), b); |
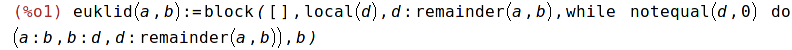
| (%i2) | euklid(20,12); |
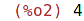
Funkce, ktera vrací největší mocnimu dvou menší nebo rovnou zadanému n.
| (%i3) |
binpow(n):=block([], local (x,m), x:0, m:n, while m>=1 do (m:m/2,x:x+1), x-1); |
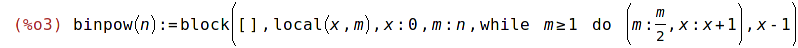
| (%i4) | binpow(8); |

| (%i5) | for n:1 thru 8 do print(n, binpow(n)); |
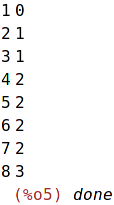
if cond_1 then expr_1 else expr_0
| (%i6) | x : -2; |
| (%i7) | if x < 0 then 0 else 1; |

| (%i8) | x : %pi; |

| (%i9) | if x < 0 then 0 else 1; |

if cond_1 then expr_1 elseif cond_2 then expr_2 elseif ... else expr_0
| (%i10) | if x < 0 then -1 elseif x = 0 then 0 else 1; |

| (%i11) | x : 0; |

| (%i12) | if x < 0 then -1 elseif x = 0 then 0 else 1; |
Následující příkaz vyplňuje horní trojúhelníkovou matici řádkovými indexy,
část pod hlavní diagonálou sloupcovými indexy a hlavní diagonálu jedničkami.
| (%i13) |
for i:1 thru 4 do for j:1 thru 4 do if i else A[i,j]:1; |
| (%i14) | listarray(A); |
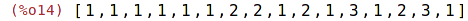
| (%i15) | arrayinfo(A); |

Nalezne první hodnotu, která není prvočíslo v posloupnosti 2^i-1, i=3,5,7,..
a jakmile ji najde, přeruší výpočet.
| (%i16) |
for i: 3 step 2 do if primep(2^i-1) then print(2^i-1, "je prvocislo") else return(2^i-1); |

2 Uživatelem definované funkce
Jednoduchý program v Maximě není nic jiného než posloupnost příkazů, např.
| (%i17) |
tangent(fn, x) := diff(fn(x), x) / ((diff(fn(x), x) * diff(fn (x), x))^(1/2)); |
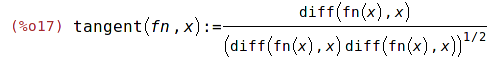
Tento zápis má jednu nevýhodu, třikrát zde počítáme tu samou derivaci.
Výhodnější je tento zápis.
| (%i18) |
tangent(fn, x) := block ( [df: diff(fn(x), x)], df / (df * df)^(1/2) ); |
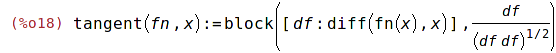
Příkaz block je vlastně tělem procedury, proměnné definované uvnitř jsou lokálními
proměnnými.
| (%i19) |
max3(a,b,c) := block([], print("nalezeni maxima z cisel ",a,b,c), if a if b |
Procedura vrací poslední vyhodnocenou hodnotu.
| (%i20) | max3(3,2,1); |

| (%i21) | save("/home_zam/plch/vyuka/maxima/maximum", max3); |
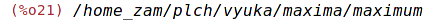
Zápis je proveden v jazyce LISP.
| (%i22) | kill(all); |
| (%i1) | load("/home_zam/plch/vyuka/maxima/maximum"); |
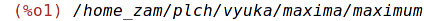
| (%i2) | max3(3,2,1); |

| (%i3) | kill(max3); |
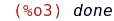
Program (proceduru) můžeme napsat i textovým editorem, pak k jejímu načtení
použijeme příkaz batch.
| (%i4) | batch("/home_zam/plch/vyuka/maxima/procedura.mac"); |

| (%i6) | max3(2,3,1); |

Procedury s proměnným počtem parametrů
| (%i7) |
prog([l]) := block([], print ("l se sklada z", l, "a pocet prvku je", length(l)))$ |
| (%i8) | prog(a,b,c,d); |
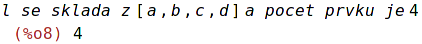
| (%i9) | kill(all); |
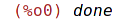
| (%i1) |
maxN([l]):=block([result], if length(l)>0 then result:l[1], for i:2 thru length(l) do if l[i]>result then result:l[i], return(result))$ |
| (%i2) | maxN(9,2,3,4,5.0); |
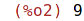
| (%i3) | result; |
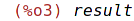
Lokální proměnné
| (%i4) | g(x):=1-x; |
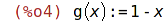
| (%i5) | g(100); |
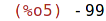
| (%i6) | block (local (g), g(x) := 2 * x, g(100)); |
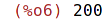
| (%i7) | g(100); |